本学习笔记是对 nanotron/ultrascale-playbook 的学习记录，该书涵盖分布式训练、并行技术以及一些优化策略。本文章是该系列笔记的第二篇，对应原书附录 A0: Parallel Programming Crash Course 一章。

后续会开始学习分布式训练相关知识，为此需要在机器之间进行权重、梯度以及数据的通信和同步。为了实现这一目标需要使用一些并行编程操作，例如 broadcast、all reduce、scatter 等，首先对这部分进行介绍，如果读者已经对这部分的内容比较熟悉，可以直接跳过本篇内容。

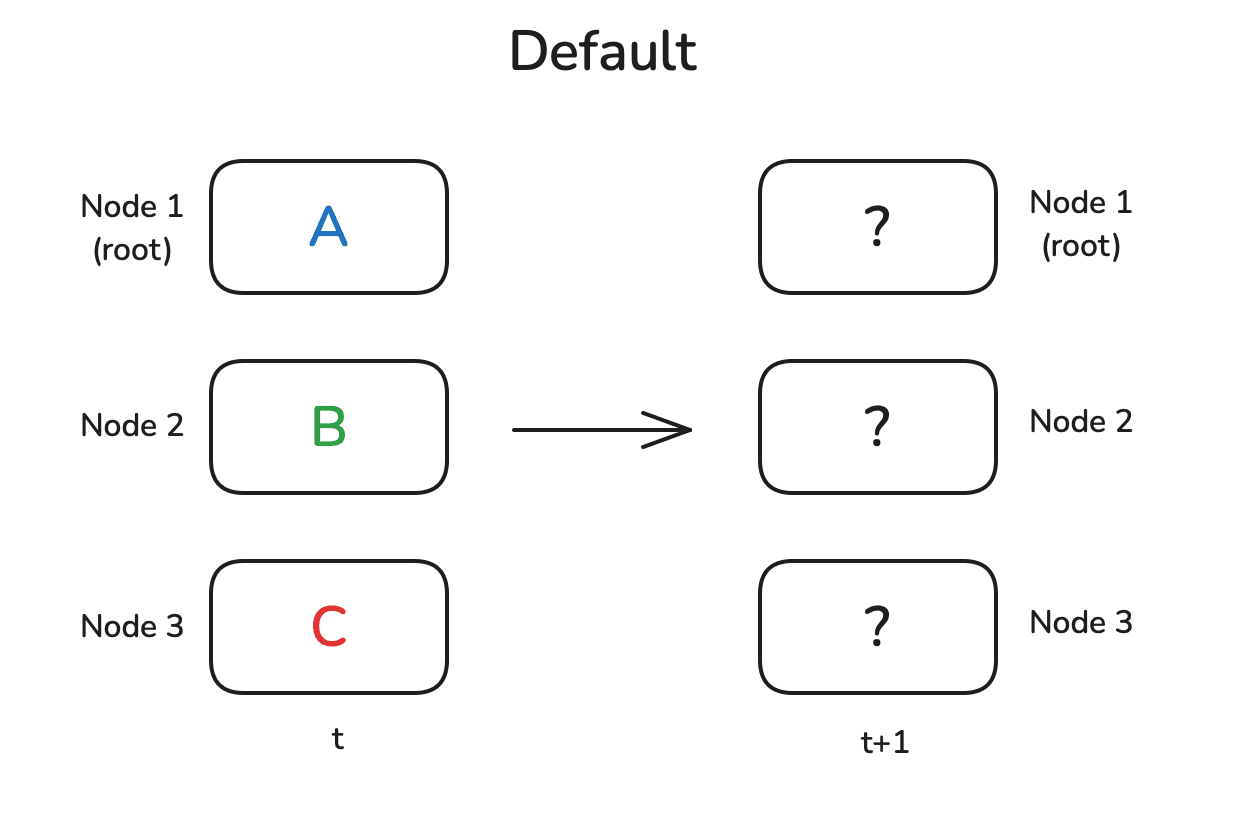
一般情况下，训练时会有多个独立的节点，这些节点可以是 CPU 核心，也可以是 GPU 或者其他节点。每个节点分别执行一些计算，然后将其结果同步到其他的节点或将这些结果全部相加来得到总体结果，如下图所示。通常来说会有一个地位较高的节点来扮演核心的角色，这里用根节点来表示，这个节点是这些操作的目标或者源头。

并行计算示意图

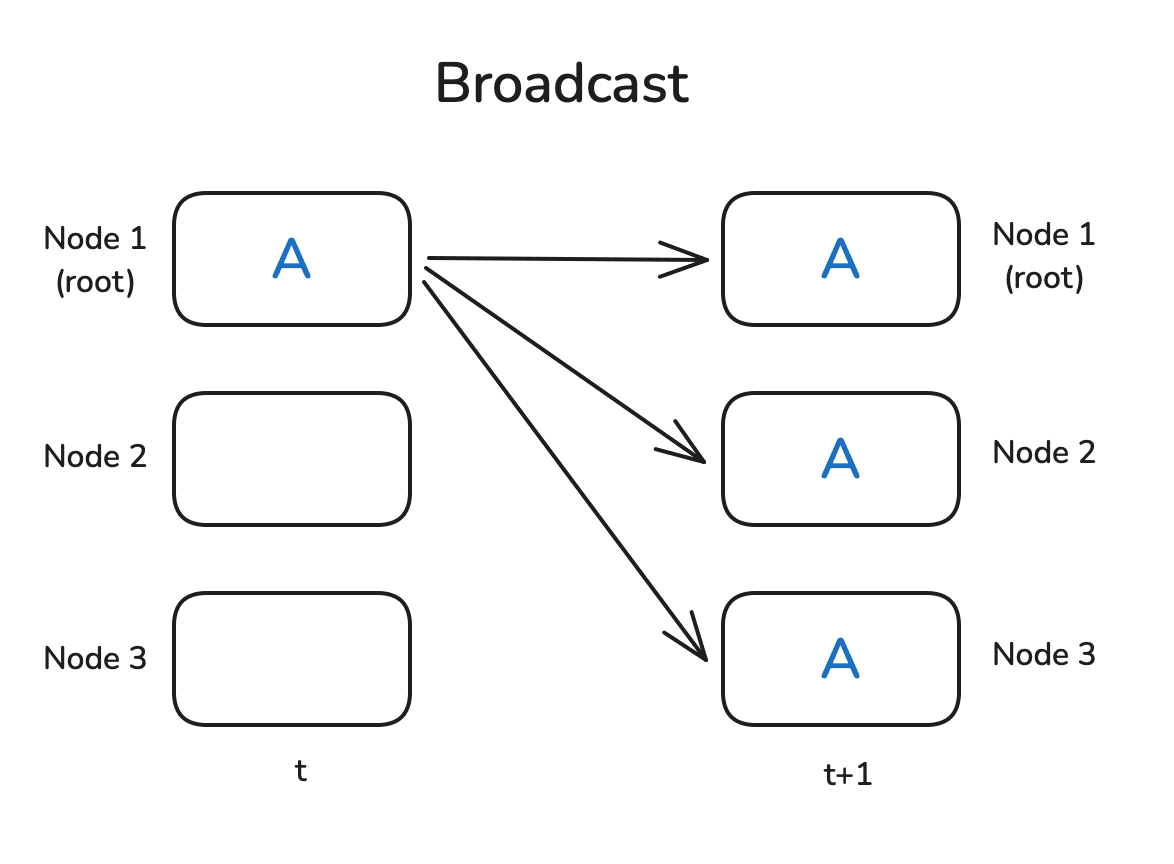
Broadcast/广播

首先是最简单的广播操作。想像这样一个场景：你在节点 1 上初始化了一些数据，现在你希望将这些数据发送给所有的其他节点，以便这些节点基于这些数据进行计算。广播操作就是为此而生：

广播操作

Pytorch 提供了原生的并行化操作，因此可以快速地实现一个 demo。我们首先需要使用 dist.init_process_group 初始化一个进程组。在进程组初始化时，其会确定有多少个节点，并为每个节点分配一个序号（也就是 rank，其可以使用 dist.get_rank 获取），最后在节点之间建立连接。

下面是一个示例，首先在 0 号进程上初始化一个非零的张量，而在其他进程中初始化全零张量，随后使用广播操作将 0 号进程上的张量分发给其他所有进程：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import torch
import torch.distributed as dist

def init_process():
    dist.init_process_group(backend='nccl')
    torch.cuda.set_device(dist.get_rank())
    
def example_broadcast():
    if dist.get_rank() == 0:
        tensor = torch.tensor([1, 2, 3, 4, 5], dtype=torch.float32).cuda()
    else:
        tensor = torch.zeros(5, dtype=torch.float32).cuda()
    print(f"Before broadcast on rank {dist.get_rank()}: {tensor}")
    dist.broadcast(tensor, src=0)
    print(f"After broadcast on rank {dist.get_rank()}: {tensor}")
    
init_process()
example_broadcats()

你可以使用 torchrun --nproc_per_node=3 dist_op.py 来运行上述脚本（为此你需要三块 GPU，或者相应地更改 nproc_per_node 的值），运行后会输出以下内容：

1
2
3
4
5
6
7
Before broadcast on rank 0: tensor([1., 2., 3., 4., 5.], device='cuda:0')
Before broadcast on rank 1: tensor([0., 0., 0., 0., 0.], device='cuda:1')
Before broadcast on rank 2: tensor([0., 0., 0., 0., 0.], device='cuda:2')

After broadcast on rank 0: tensor([1., 2., 3., 4., 5.], device='cuda:0')
After broadcast on rank 1: tensor([1., 2., 3., 4., 5.], device='cuda:1')
After broadcast on rank 2: tensor([1., 2., 3., 4., 5.], device='cuda:2')

请注意，不同 rank 的消息打印顺序可能是乱的，因为我们无法控制哪个 print 语句先执行（这里为了可读性，对输出进行了排序）。

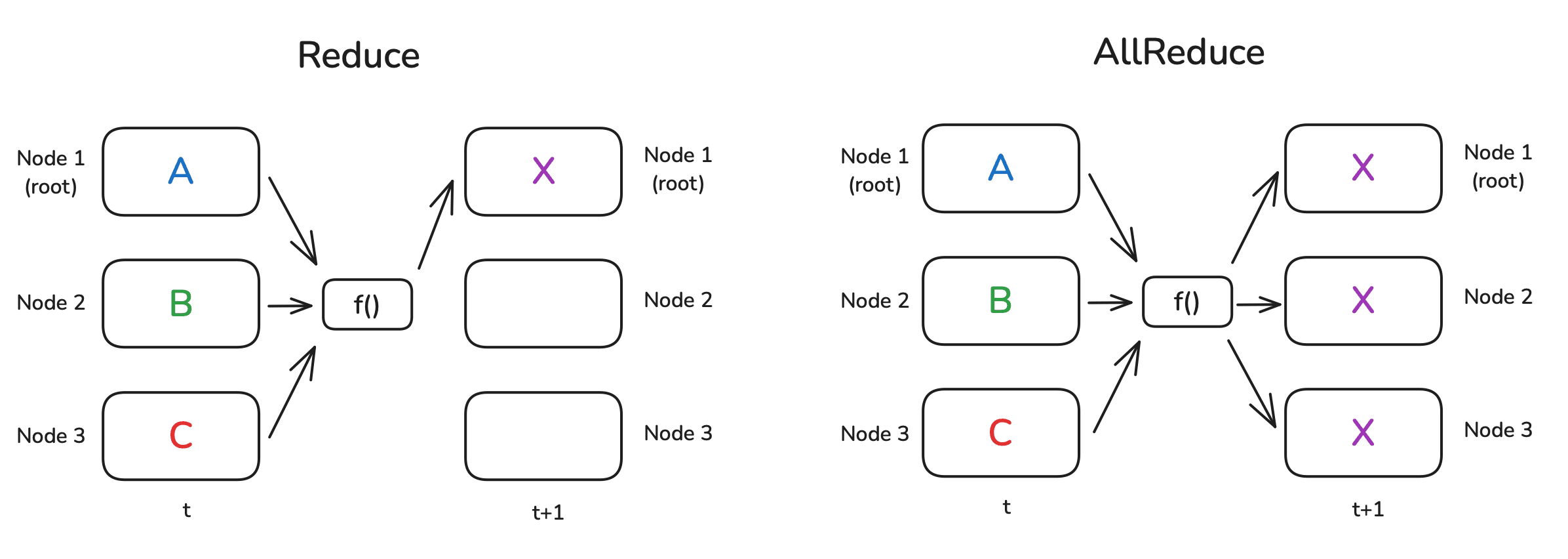
Reduce/规约 & AllReduce/全规约

Reduce 是分布式计算中最常用的操作之一。想像这样一个场景：你在不同的节点上完成了一些计算，现在你希望计算出这些结果的和或者平均值。Reduce 操作就是为了汇集不同节点上的数据，如果使用 Reduce，结果只会发送给跟节点；如果使用 All Reduce，结果会广播给所有节点。

Reduce 与 All Reduce

通常来说，为了实现这个结果，这些节点会组织成环形或树形结构，且每个节点都会参与计算。举个简单的例子：假设我们需要计算每个节点上数字的总和，并且节点以环形结构连接。那么第一个节点将其数字发送给相邻的节点，相邻的节点将其自己的数字与收到的数字相加，然后转发给下一个节点。在环绕一圈后，第一个节点将收到所有数值的总和。

当然我们在实现的时候并不需要手动管理上述的过程，只需使用 op=dist.ReduceOp.SUM 即可指定使用的操作（具体请参考 Pytorch 官方文档）：

1
2
3
4
5
6
7
8
def example_reduce():
    tensor = torch.tensor([dist.get_rank() + 1] * 5, dtype=torch.float32).cuda()
    print(f"Before reduce on rank {dist.get_rank()}: {tensor}")
    dist.reduce(tensor, dst=0, op=dist.ReduceOp.SUM)
    print(f"After reduce on rank {rank}: {tensor}")
    
init_process()
example_reduce()

请注意，在 Reduce 操作中，只有 dst 节点上的张量被更新了：

1
2
3
4
5
6
7
Before reduce on rank 0: tensor([1., 1., 1., 1., 1.], device='cuda:0')
Before reduce on rank 1: tensor([2., 2., 2., 2., 2.], device='cuda:1')
Before reduce on rank 2: tensor([3., 3., 3., 3., 3.], device='cuda:2')

After reduce on rank 0: tensor([6., 6., 6., 6., 6.], device='cuda:0')
After reduce on rank 1: tensor([2., 2., 2., 2., 2.], device='cuda:1')
After reduce on rank 2: tensor([3., 3., 3., 3., 3.], device='cuda:2')

类似地，我们可以使用 All Reduce 操作（这种情况下我们不需要指定目标 rank）：

1
2
3
4
5
6
7
8
def example_all_reduce():
    tensor = torch.tensor([dist.get_rank() + 1] * 5, dtype=torch.float32).cuda()
    print(f"Before all_reduce on rank {dist.get_rank()}: {tensor}")
    dist.all_reduce(tensor, op=dist.ReduceOp.SUM)
    print(f"After all_reduce on rank {dist.get_rank()}: {tensor}")
    
init_process()
example_all_reduce()

在这种情况下，所有节点都将收到结果：

1
2
3
4
5
6
7
Before all_reduce on rank 0: tensor([1., 1., 1., 1., 1.], device='cuda:0')
Before all_reduce on rank 1: tensor([2., 2., 2., 2., 2.], device='cuda:1')
Before all_reduce on rank 2: tensor([3., 3., 3., 3., 3.], device='cuda:2')

After all_reduce on rank 0: tensor([6., 6., 6., 6., 6.], device='cuda:0')
After all_reduce on rank 1: tensor([6., 6., 6., 6., 6.], device='cuda:1')
After all_reduce on rank 2: tensor([6., 6., 6., 6., 6.], device='cuda:2')

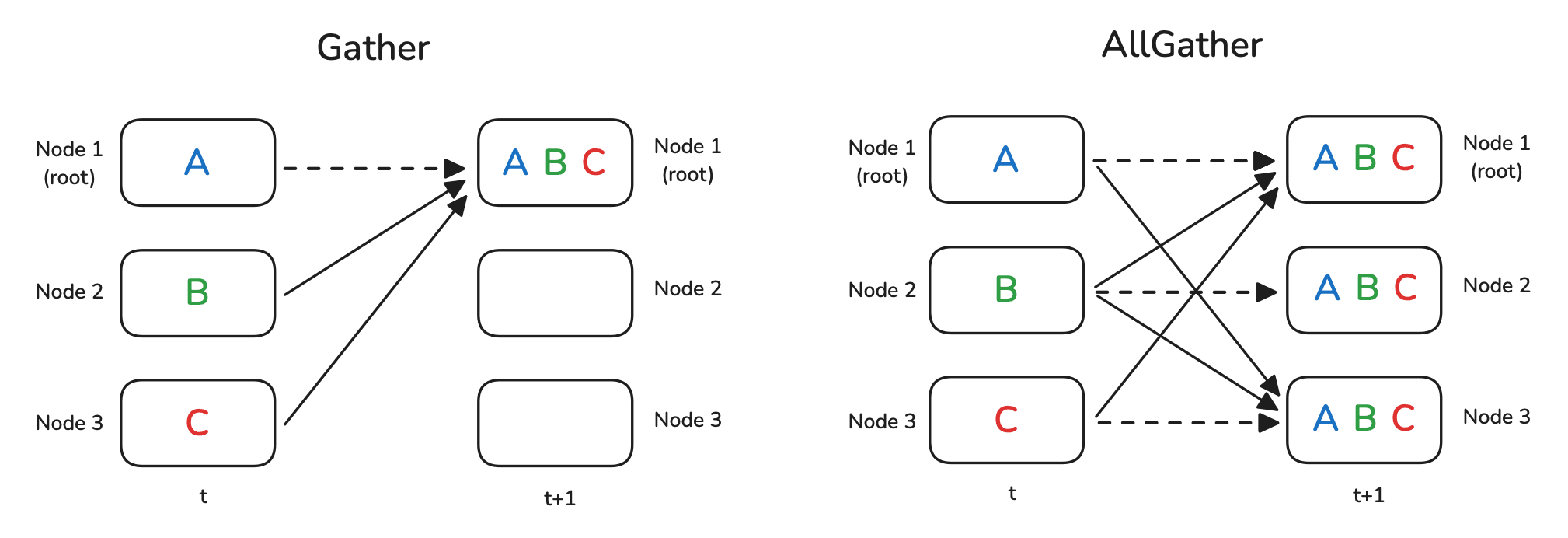
Gather/收集 & AllGather/全收集

Gather 和 All Gather 操作比较类似于 Broadcast。对于 Gather 来说，是把所有节点上的数据都收集到同一个节点上；对于 All Gather 来说，则是所有节点都收集到全部的数据。从下边的图可以有一个直观感受，图中的虚线实际上并没有移动数据，因为对应的数据已经存在于本节点上：

Gather 与 All Gather

在使用 Gather 操作时，需要创建一个容器来存储收集到的张量，这里是使用了一个 list 对象：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def example_gather():
    tensor = torch.tensor([dist.get_rank() + 1] * 5, dtype=torch.float32).cuda()
    if dist.get_rank() == 0:
        gather_list = [
            torch.zeros(5, dtype=torch.float32).cuda()
            for _ in range(dist.get_world_size())
        ]
    else:
        gather_list = None
    print(f"Before gather on rank {dist.get_rank()}: {tensor}")
    dist.gather(tensor, gather_list, dst=0)
    if dist.get_rank() == 0:
        print(f"After gather on rank 0: {gather_list}")
    
init_process()
example_gather()

可以看到 gather_list 中的确收集到了所有的张量：

1
2
3
4
5
6
7
Before gather on rank 0: tensor([1., 1., 1., 1., 1.], device='cuda:0')
Before gather on rank 1: tensor([2., 2., 2., 2., 2.], device='cuda:1')
Before gather on rank 2: tensor([3., 3., 3., 3., 3.], device='cuda:2')

After gather on rank 0: [tensor([1., 1., 1., 1., 1.], device='cuda:0'),
                         tensor([2., 2., 2., 2., 2.], device='cuda:0'),
                         tensor([3., 3., 3., 3., 3.], device='cuda:0')]

对于 All Gather 操作，由于所有节点都要接收结果，所以需要在每个节点上都初始化容器：

1
2
3
4
5
6
7
8
9
10
11
12
def example_all_gather():
    tensor = torch.tensor([dist.get_rank() + 1] * 5, dtype=torch.float32).cuda()
    gather_list = [
        torch.zeros(5, dtype=torch.float32).cuda()
        for _ in range(dist.get_world_size())
    ]
    print(f"Before all_gather on rank {dist.get_rank()}: {tensor}")
    dist.all_gather(gather_list, tensor)
    print(f"After all_gather on rank {dist.get_rank()}: {gather_list}")
    
init_process()
example_all_gather()

现在可以看到每个节点都收集到了所有的数据：

1
2
3
4
5
6
7
8
9
10
11
12
13
Before all_gather on rank 0: tensor([1., 1., 1., 1., 1.], device='cuda:0')
Before all_gather on rank 1: tensor([2., 2., 2., 2., 2.], device='cuda:1')
Before all_gather on rank 2: tensor([3., 3., 3., 3., 3.], device='cuda:2')

After all_gather on rank 0: [tensor([1., 1., 1., 1., 1.], device='cuda:0'),
                             tensor([2., 2., 2., 2., 2.], device='cuda:0'),
                             tensor([3., 3., 3., 3., 3.], device='cuda:0')]
After all_gather on rank 1: [tensor([1., 1., 1., 1., 1.], device='cuda:1'),
                             tensor([2., 2., 2., 2., 2.], device='cuda:0'),
                             tensor([3., 3., 3., 3., 3.], device='cuda:0')]
After all_gather on rank 2: [tensor([1., 1., 1., 1., 1.], device='cuda:2'),
                             tensor([2., 2., 2., 2., 2.], device='cuda:2'),
                             tensor([3., 3., 3., 3., 3.], device='cuda:2')]

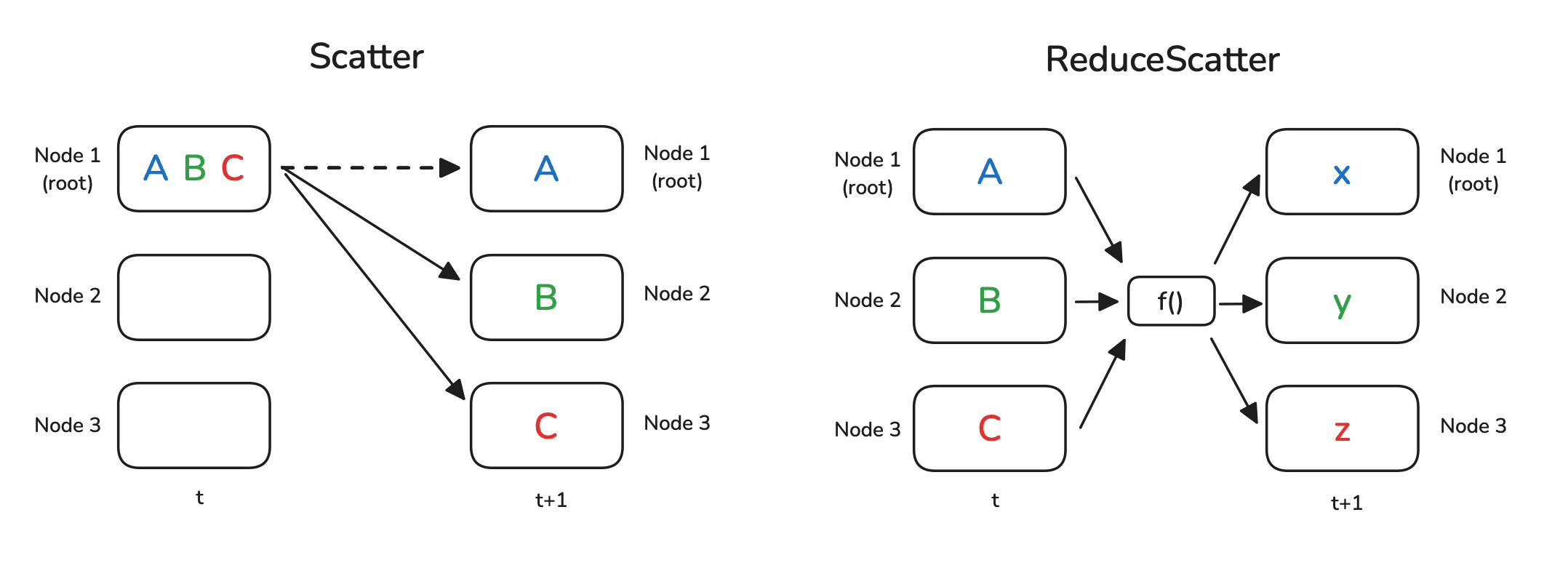
Scatter/散发 & ReduceScatter/规约散发

顾名思义，Scatter/散发就是将一个节点上的数据散发到所有节点上。注意这里的散发不同于广播，广播会将完整的数据传输到其他节点上，而散发则是将数据先进行切片，再把每个切片分别传输到每个节点。也就是说，Scatter 是 Gather 的逆操作。

ReduceScatter 的操作则稍微复杂一点，这个操作相当于先进行 Reduce 再进行 Scatter，最终的结果相当于把每个结点上的数据进行某种映射。用语言描述这个过程或许比较复杂，不过直接看图就很直观：

Scatter 和 ReduceScatter

在实现时，Scatter 的写法和 Gather 相反：我们不是准备一个张量列表作为目标，而是将源数据准备成一个我们想要分发的张量列表，除此之外还需要指定 src：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def example_scatter():
    if dist.get_rank() == 0:
        scatter_list = [
            torch.tensor([i + 1] * 5, dtype=torch.float32).cuda()
            for i in range(dist.get_world_size())
        ]
        print(f"Rank 0: Tensor to scatter: {scatter_list}")
    else:
        scatter_list = None
    tensor = torch.zeros(5, dtype=torch.float32).cuda()
    print(f"Before scatter on rank {dist.get_rank()}: {tensor}")
    dist.scatter(tensor, scatter_list, src=0)
    print(f"After scatter on rank {dist.get_rank()}: {tensor}")
    
init_process()
example_scatter()

结果是空的张量被 scatter_list 的内容填充了：

1
2
3
4
5
6
7
8
9
10
Rank 0: Tensor to scatter: [tensor([1., 1., 1., 1., 1.], device='cuda:0'),
                            tensor([2., 2., 2., 2., 2.], device='cuda:0'),
                            tensor([3., 3., 3., 3., 3.], device='cuda:0')]
Before scatter on rank 0: tensor([0., 0., 0., 0., 0.], device='cuda:0')
Before scatter on rank 1: tensor([0., 0., 0., 0., 0.], device='cuda:1')
Before scatter on rank 2: tensor([0., 0., 0., 0., 0.], device='cuda:2')

After scatter on rank 0: tensor([1., 1., 1., 1., 1.], device='cuda:0')
After scatter on rank 1: tensor([2., 2., 2., 2., 2.], device='cuda:1')
After scatter on rank 2: tensor([3., 3., 3., 3., 3.], device='cuda:2')

为了展示 ReduceScatter 的逻辑，我们在每个节点上创建一个由两个元素组成的向量的列表：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def example_reduce_scatter():
    rank = dist.get_rank()
    world_size = dist.get_world_size()
    input_tensor = [
        torch.tensor([(rank + 1) * i for i in range(1, 3)], dtype=torch.float32).cuda()**(j+1) 
        for j in range(world_size)
    ]
    output_tensor = torch.zeros(2, dtype=torch.float32).cuda()
    
    print(f"Before ReduceScatter on rank {rank}: {input_tensor}")
    dist.reduce_scatter(output_tensor, input_tensor, op=dist.ReduceOp.SUM)
    print(f"After ReduceScatter on rank {rank}: {output_tensor}")    
    
init_process()
example_reduce_scatter()

直接看表达式可能不太容易理解，不过通过打印出来的结果可以大致理解数据创建的规则。从结果也可以发现 ReduceScatter 操作的作用——第一个 rank 接收了来自每个节点的第一个张量的和，第二个 rank 接收了来自每个节点的第二个张量的和，依此类推：

1
2
3
4
5
6
7
8
9
10
11
12
13
Before ReduceScatter on rank 0: [tensor([1., 2.], device='cuda:0'),
                                 tensor([1., 4.], device='cuda:0'),
                                 tensor([1., 8.], device='cuda:0')]
Before ReduceScatter on rank 1: [tensor([2., 4.], device='cuda:1'),
                                 tensor([4., 16.], device='cuda:1'),
                                 tensor([8., 64.], device='cuda:1')]
Before ReduceScatter on rank 2: [tensor([3., 6.], device='cuda:2'),
                                 tensor([9., 36.], device='cuda:2'),
                                 tensor([27., 216.], device='cuda:2')]

After ReduceScatter on rank 0: tensor([6., 12.], device='cuda:0')
After ReduceScatter on rank 1: tensor([14., 56.], device='cuda:1')
After ReduceScatter on rank 2: tensor([36., 288.], device='cuda:2')

Ring AllReduce/环形全规约

和上面的几个操作不同，Ring AllReduce 并不是某种操作，而是 AllReduce 的一种特定的实现，这种实现为可拓展性进行了优化。它不是让所有设备直接相互通信（因为可能造成通信瓶颈），而是分解为两个关键步骤：ReduceScatter 和 AllGather。工作原理如下：

  1. ReduceScatter

    • 每个设备将其数据分成 N 个块（其中 N 是 GPU 的数量），并将一个块发送给它的邻居。同时，每个设备从其另一个邻居接收一个块。
    • 当每个设备收到一个块时，它将自己对应的块加到（归约）收到的块上。
    • 这个过程在环上持续进行，直到每个设备都持有一个完全归约过的块，该块代表了所有设备上该块数据的总和。

  2. AllGather

    • 现在，每个设备需要从其他设备收集完全归约过的块。

    • 每个设备将其归约过的块发送给它的邻居，并从另一个邻居接收归约过的块。

    • 设备继续转发它们收到的块，直到每个设备都拥有所有完全归约过的块，从而使每个设备都获得了完整、求和后的数据。

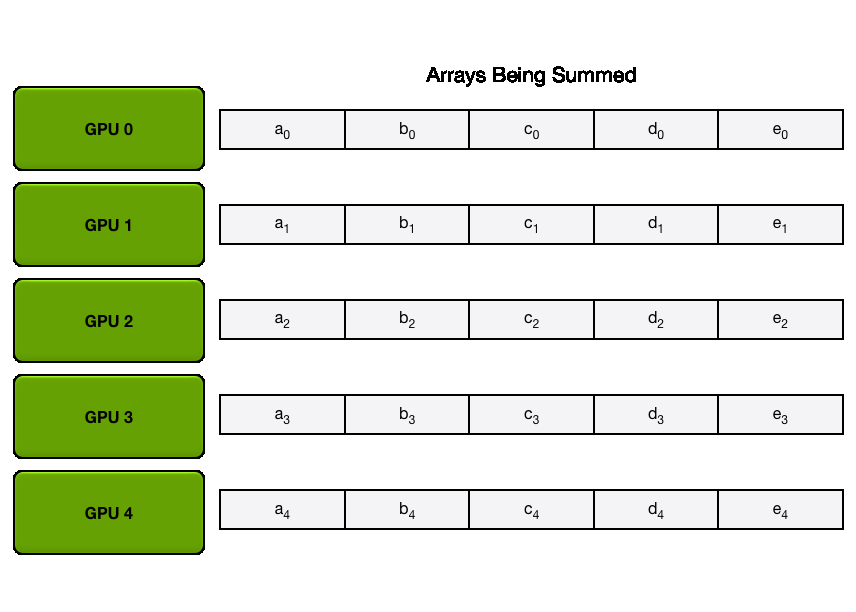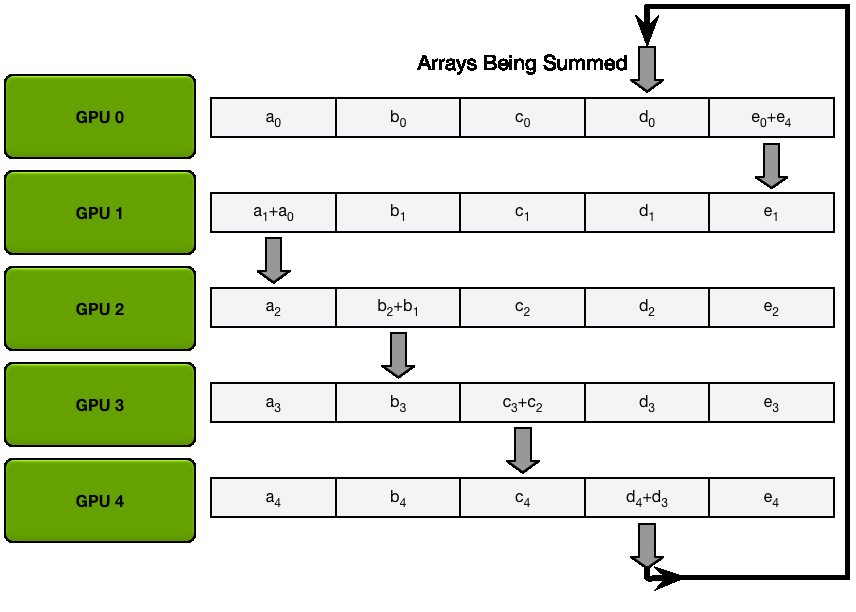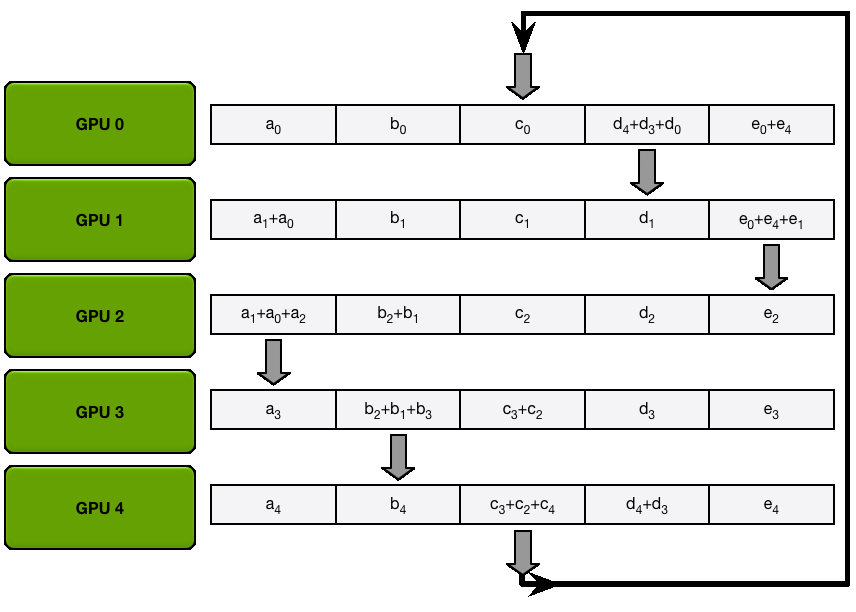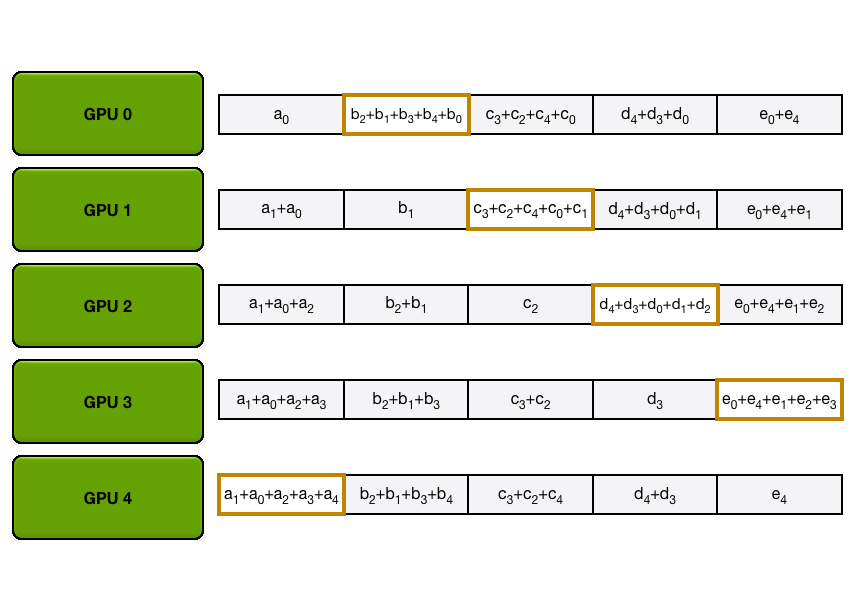
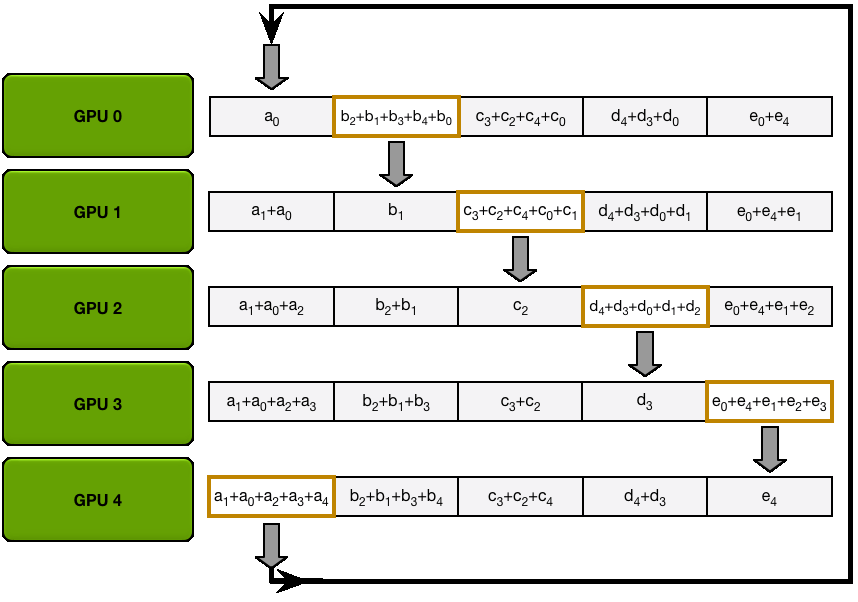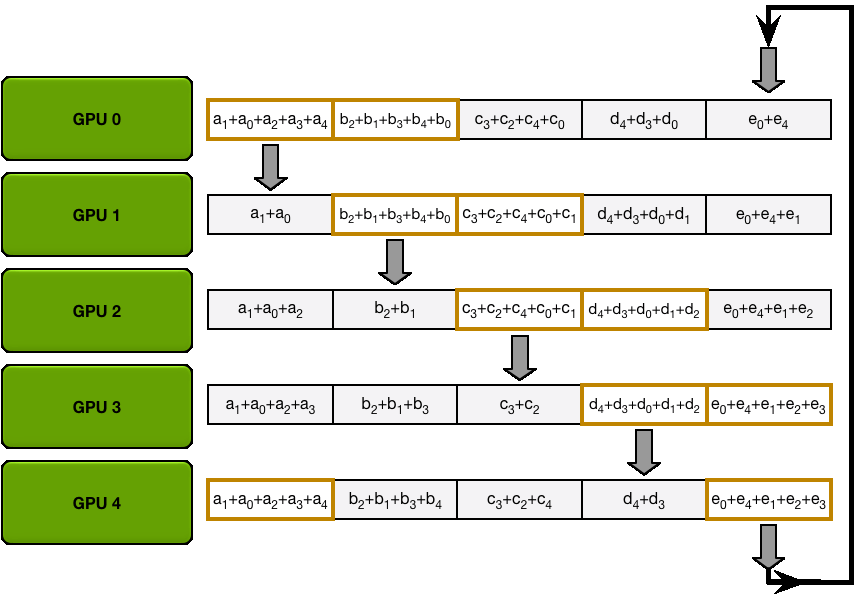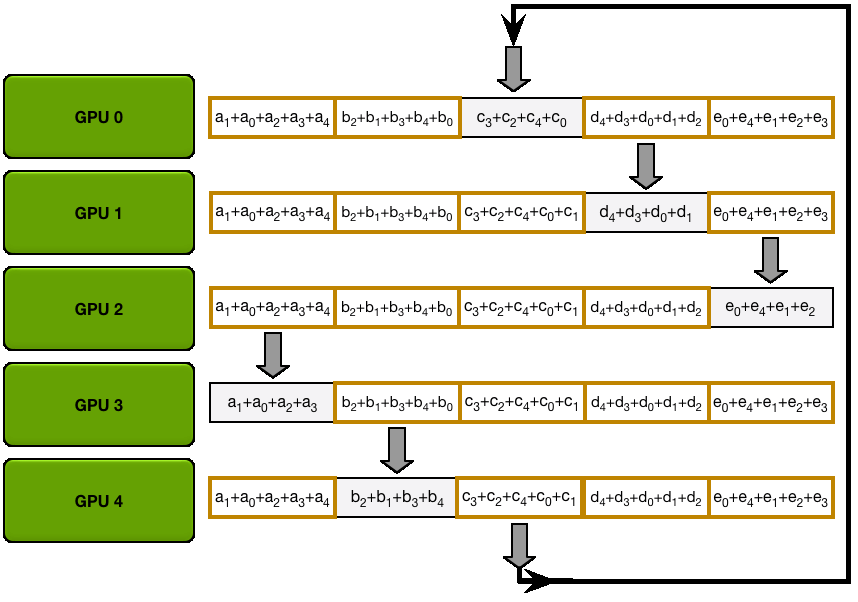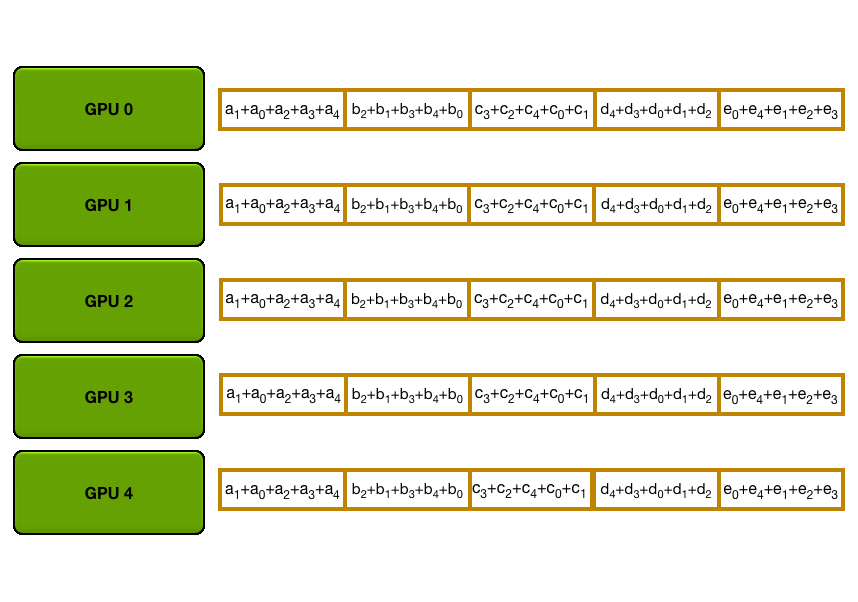
这个过程可以用下面的动图来展示。假设我们有 5 个 GPU，每个 GPU 上都有一个长度为 5 的张量。第一个动图展示的是 ReduceScatter 步骤，最后，每个 GPU 接收到某个数据块（橙色矩形）的归约结果。

Ring AllReduce 的第一步：ReduceScatter

下一个动图展示的是 AllGather 步骤，最后，每个 GPU 获得了 AllReduce 操作的完整结果：

Ring AllReduce 的第二步：AllGather

可以发现在 ReduceScatter 和 AllGather 两个步骤中 \(N\) 个 GPU 中的每个都发送并接收了 \(N-1\) 次数据。每个 GPU 每次数据传输发送的数据量为 \(K/N\)，其中 \(K\) 是序列的长度。因此 GPU 在这个过程中发送和接收的数据总量为 \(2\times(N-1)\times K/N\)。当 GPU 的数量 \(K\) 比较大的时候，每个 GPU 发送和接收的数据量近似为 \(2K\)。

如果形象地解释一下，使用 ReduceScatter+AllGather 的方式实现 AllReduce，数据只在 GPU 之间「转了一圈」；而如果直接使用环状通信的方式实现 AllReduce，数据需要「转两圈」，因此这种实现方式可以节约大约一半的 GPU 带宽。

Barrier/屏障

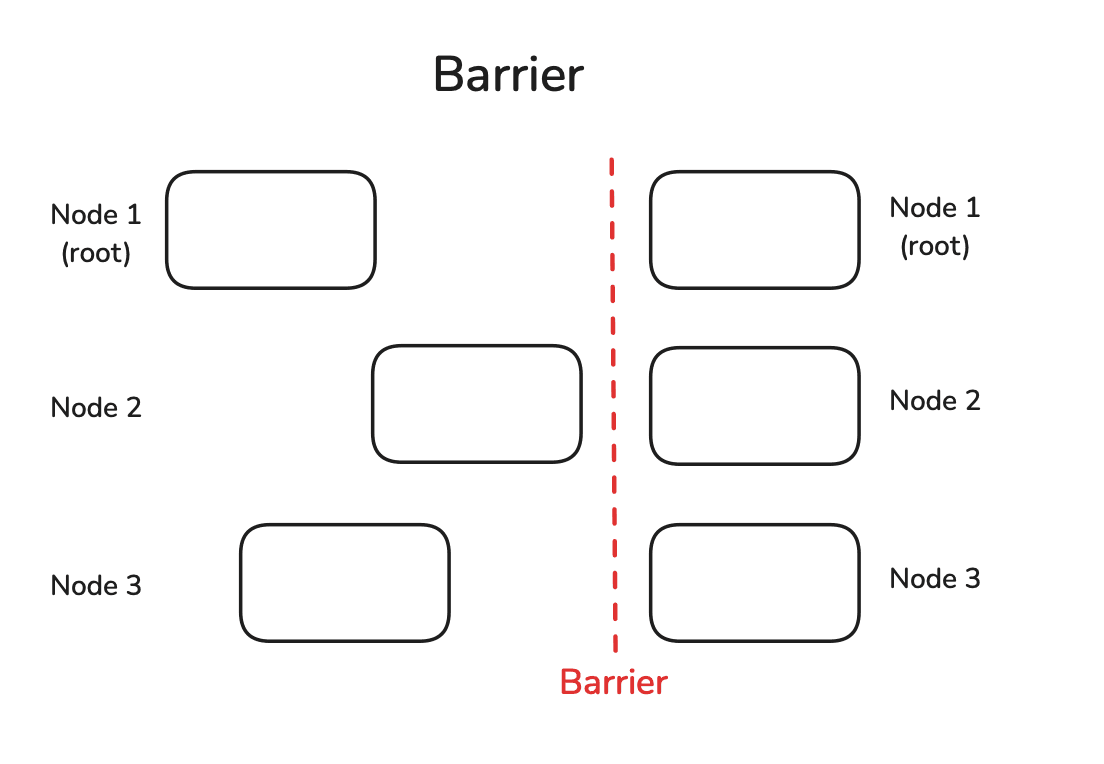
Barrier 是一个简单的同步所有节点的操作。想像一个这样的场景，你有一批数据需要分布在不同的 GPU 上进行推理，并在所有数据都推理完成后计算准确率，但不同 GPU 需要的运行时间不同，所以需要在计算准确率之前等待所有 GPU 上的推理都运行完成，这就需要用到 Barrier。在一个 Barrier 处，直到所有节点都到达它，它才会被解除。只有这样，节点才被允许继续进行后续的计算：

Barrier 示意图

我们可以通过在每个节点上设置不同的睡眠时间来轻松模拟延迟的节点，并观察它们全部通过 Barrier 需要多长时间：

1
2
3
4
5
6
7
8
9
10
11
12
13
import time

def example_barrier():
    rank = dist.get_rank()
    t_start = time.time()
    
    print(f"Rank {rank} sleeps {rank} seconds.")
    time.sleep(rank)  # 模拟不同的处理时间
    dist.barrier()
    print(f"Rank {rank} after barrier time delta: {time.time()-t_start:.4f}")
    
init_process()
example_barrier()

我们可以看到，尽管第一个 rank 完全没有睡眠，但它也花了 2 秒钟才通过屏障：

1
2
3
4
5
6
7
Rank 0 sleeps 0 seconds.
Rank 1 sleeps 1 seconds.
Rank 2 sleeps 2 seconds.

Rank 0 after barrier time delta: 2.0025
Rank 1 after barrier time delta: 2.0025
Rank 2 after barrier time delta: 2.0024

在并行计算时，需要谨慎使用这种同步所有节点的操作，因为这违背了并行独立操作的初衷，可能会减慢整个处理过程。在许多情况下，不同节点之间的同步是非必要的，所以在使用之前请谨慎考虑。

总之并行计算的一些常用操作就总结到这里了，掌握了这些知识，相信在后续的并行训练策略学习中会更加得心应手。