本学习笔记是对 nanotron/ultrascale-playbook 的学习记录，该书涵盖分布式训练、并行技术以及一些优化策略。本文章是该系列笔记的第一篇，对应原书 First Steps: Training on One GPU 一章。

在开始学习分布式训练前，不妨先快速回顾一下模型训练的基础知识。在单 GPU 上训练模型时，训练通常包含三个步骤：

  1. 前向传播：将输入传递至模型并产生输出；
  2. 反向传播：进行梯度计算；
  3. 优化步骤：根据计算出的梯度对模型的参数进行更新。

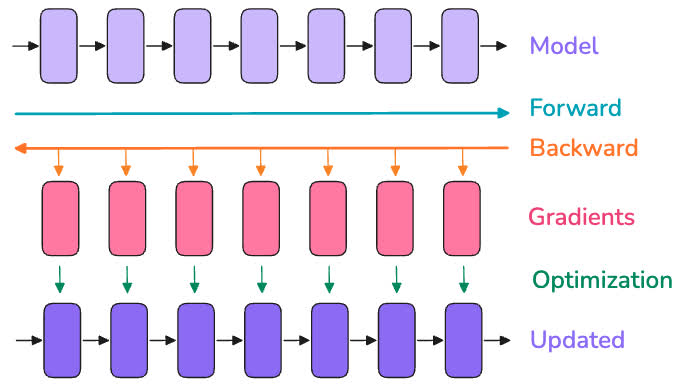
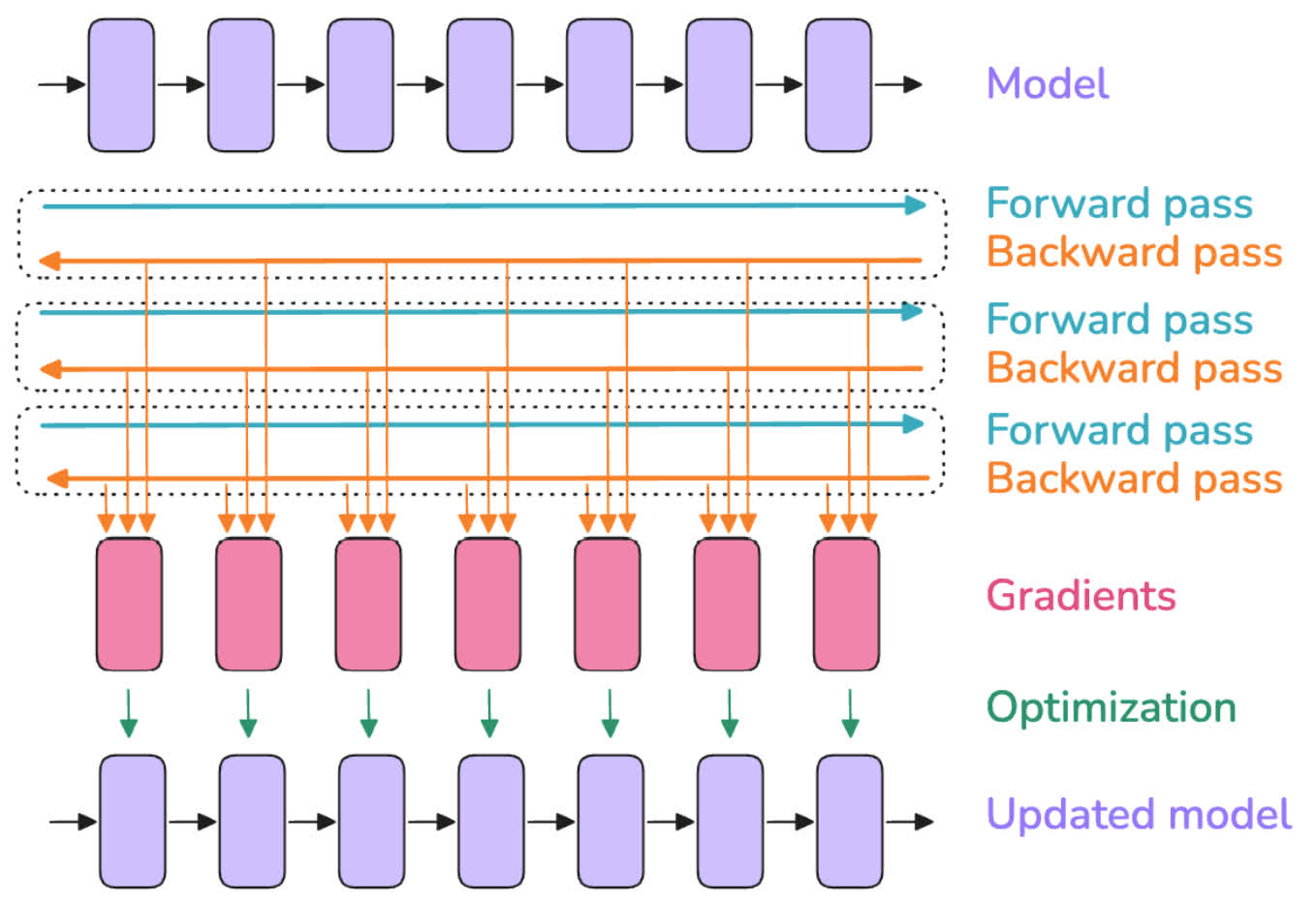
总体上来说可以用下图表示。图中第一行和最后一行的紫色框可以看作模型的不同层，黑色箭头表示了这些层的连接关系。在训练时，首先对输入进行前向传播（青色箭头），随后反向传播计算梯度（橙色箭头）。使用得到的梯度对模型的参数进行更新，可以得到优化过的模型。

模型的训练过程示意图

在模型训练过程中，batch size 是最重要的超参数之一，其影响模型训练的收敛速度以及吞吐量。具体来说，在训练初期，较小的 batch size 可以帮助模型快速地到达最佳的学习位置，然而随着训练的进行，小的 batch size 会导致梯度含有比较多的噪声，最终模型可能无法收敛到最佳性能的位置。另一个极端是，大的 batch size 虽然可以在训练过程中提供稳定的梯度，但其会降低每个训练样本的利用效率，从而减慢收敛速度，并且可能浪费计算资源。同时，batch size 也会影响训练时间，因为在对相同样本数量进行训练的前提下，小的 batch size 需要更多的优化器 step。由于优化器 step 非常耗时，所以相比大的 batch size，总体的训练时间会变长。

举例来说，在 DeepSeek-V3/R1 在训练前 469B tokens 时，batch size 逐渐从 3072 提高到 15360，随后一直保持在 15360 这个大小

在预训练 LLM 的社区中，batch size 通常不以样本数为单位，而是以 token 数为单位（即 bst = batch size tokens）。训练大模型的 batch size 和语料库大小近些年逐年上升，例如 LLaMA 1 使用了 1.4T token 以大约 4M 的 batch size 训练，而 DeepSeek 则使用了 14T token 以及大约 60M 的 batch size。

随着训练的 batch size 增大，我们遇到的第一个挑战就是 out-of-memory (OOM) 问题。当我们的显存无法容纳一整个 batch 的数据时，我们应该怎么办？为了解决这个问题，我们首先需要了解 OOM 出现的原因。

Transformer 的内存使用情况

在训练一个深度神经网络时，模型使用的内存主要由以下几部分组成：

  • 模型权重（weights）
  • 模型梯度（gradients）
  • 优化器状态（optimizer states）
  • 计算梯度所需要的激活值（activations）

在现实场景中，使用的显存通常难以精确计算，这是因为 CUDA 内核本身需要占用一些显存，这可以通过运行 import torch; torch.ones((1, 1)).to("cuda") 快速地验证。除此之外，一些缓存和中间结果也会占用显存，显存碎片化也会导致部分显存不可用（不过这个因素的影响较小，可以忽略）

上述的部分在 GPU 中以张量的形式存储，其有两个主要的属性，也就是形状和精度。张量的形状和模型本身以及输入有关；精度则有很多种不同的类型，例如 fp32、bf16、fp8 等，不同精度的数值占用的内存也不同。

测算显存使用情况

一般来说，要确定模型的显存占用，需要经验性地估计以及直接使用工具测量。下面就是 LLaMA 1B 在前四个训练 step 时的显存变化情况，可以看出显存占用并不是固定的，而是会动态变化：

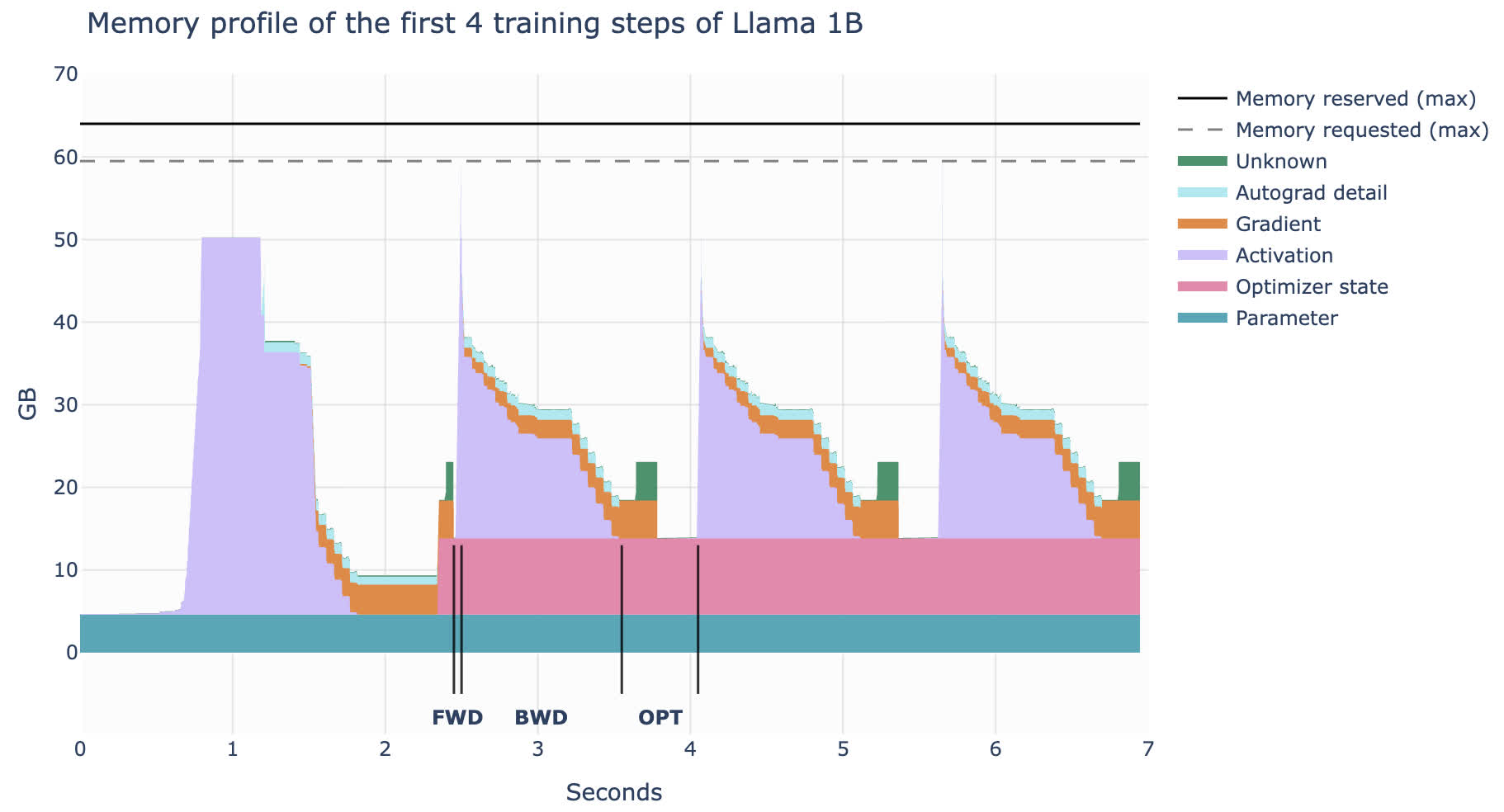
LLaMA 1B 在训练前四次迭代时的内存占用状态

首先总览一下训练过程，首先在第一次前向传播的时候激活部分快速增加，之后随着反向传播的过程，梯度逐渐被计算出来，同时存储的激活值逐渐被释放。最后优化器执行优化，在优化时需要全部的梯度均被计算出来，随后优化器的状态被更新，并开始下一次迭代。

如上图所示，第一个迭代步骤是明显有别于其他迭代步骤的，其激活值快速增加并在峰值停留了一段时间。这是因为 Pytorch 的内存管理器在进行准备工作，为内存分配作准备，从而加速后续的内存访问。在第一次迭代结束后优化器的状态出现（有时这会导致训练的第一个 iteration 成功，而随后发生 OOM 导致失败）

通过上述分析可以发现，扩大训练规模需要最大化计算效率，同时将这些内存需求保持在 GPU 的内存限制范围内。

权重/梯度/优化器状态的内存占用

权重、梯度以及优化器状态使用的内存可以比较短平快地计算出来。对于一个简单的 Transformer 架构的 LLM，其参数量可以用如下的公式计算（具体计算过程见这篇文章）： \[ N=h\times v+L\times(12\times h^2+13\times h)+2\times h \] 其中 \(h\) 是隐藏层维度，\(v\) 是词表大小，\(L\) 是模型的层数。可以发现主要的影响因素是 \(h^2\) 这一项。模型参数和梯度需要的内存大小可以直接通过参数量乘以精度对应的字节数量得到。对于全精度（即 fp32）训练，参数和梯度均占用 4 个字节，如果使用 Adam 优化器，则动量和方差均需要存储，即每个参数需要 8 字节的空间，因此有： \[ \begin{aligned} m_{params}&=4\times N\\ m_{grad}&=4\times N \\ m_{opt}&=(4+4)\times N \end{aligned} \] 对于混合精度训练的情况，例如以 bf16 的精度进行训练，则需要以 bf16 的精度存储模型参数和梯度，并以 fp32 的精度储存另一份模型参数和优化器状态。在这种情况下，内存的消耗情况为： \[ \begin{aligned} m_{params}&=2\times N\\ m_{grad}&=2\times N \\ m_{params\_fp32}&=4\times N\\ m_{opt}&=(4+4)\times N \end{aligned} \] 值得注意的是，混合精度训练本身并不节约内存（甚至可能增加内存消耗），其只是改变了不同组件之间的内存分配方式。不过其仍具有优势，因为以半精度计算前向和反向传播过程，可以：

  1. 在 GPU 上使用低精度运算，这些运算的速度更快；
  2. 减少前向传播过程中的内存占用（根据上图，峰值内存通常出现在前向过程中，因此可以降低峰值内存）

大体上来说，不同参数量对应的模型显存占用（仅包含上述的三个部分，不包含激活部分）如下表所示。可以发现当模型参数量达到 7B 时，其需要的显存大小就已经超过了现有 GPU 的内存大小（80 GiB）：

模型参数量 FP32 或 BF16 训练（保存半精度梯度） BF16 训练（保存全精度梯度）
1B 16 GiB 20 GiB
7B 112 GiB 140 GiB
70B 1120 GiB 1400 GiB
405B 6480 GiB 8100 GiB

不过目前我们仅关注能够进行单卡训练的模型，并继续讨论显存占用的大头，也就是激活部分。

激活部分的内存占用

相比于上边的三个部分，激活部分的内存占用计算方式稍微复杂一些，因为这部分和模型的输入有关。经过推导（过程见这篇论文）可以得知混合精度训练时这部分的内存占用可以用下面的公式计算： \[ m_{act}=L\times seq\times bs\times h\times(34+\frac{5\times n_{heads}\times seq}h) \] 其中 \(L\) 是模型的层数，\(seq\) 是序列的长度，\(bs\) 是每个 batch 的 sample 数量，\(h\) 是模型的隐藏层为度，\(n_{heads}\) 是模型的 head 的数量。

可以发现，对于给定的模型，其激活部分的内存使用量和 batch size 呈现线性关系，和序列的长度呈现二次关系。举例来说，对于 batch size 为 1 情况下的 LLaMA 系列模型，情况如下图所示。从图中可以发现，对于短的序列或小的 batch，激活部分的内存占用几乎可以忽略不计，单从大约 2-4k token 开始，其开始占用大量内存，而模型参数、梯度、优化器状态的内存占用和批次大小基本无关。

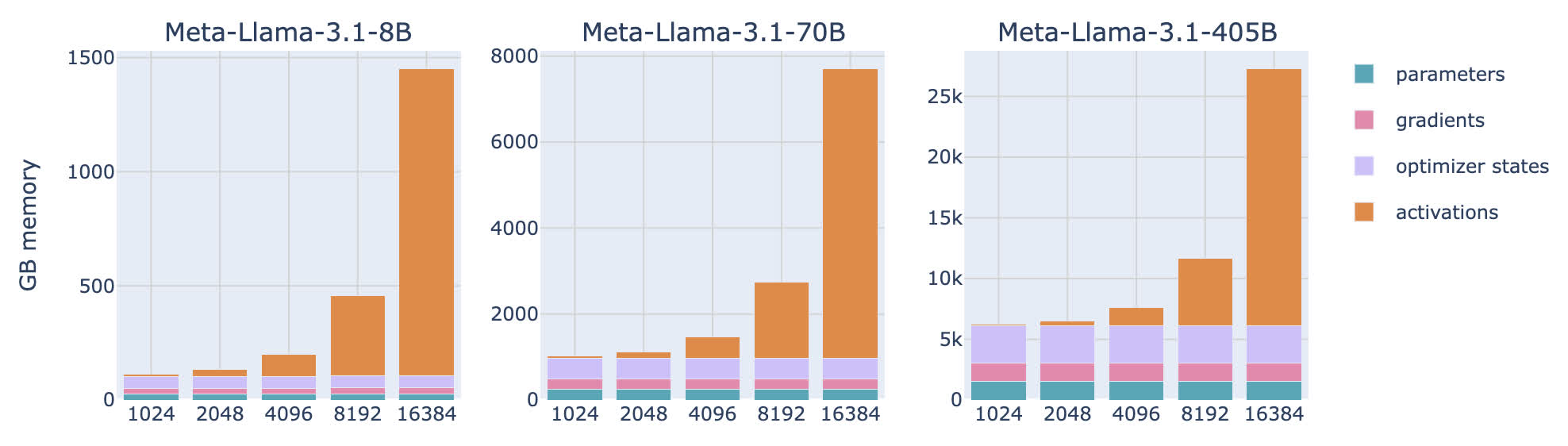
LLaMA 系列模型的内存占用随 token 数量的变化

随着输入 token 数量的增长，激活部分所需的显存也会爆炸式增加。为了解决这个问题，我们需要引入一种新的技术，叫做 gradient checkpointing。

Gradient Checkpointing

在原文中，这种技术的名字也叫做 activation recomputation 或 rematerialization，不过 gradient checkpointing 应该更被人熟知，所以本小节的标题改为了后者。这种技术的核心思想是用计算换空间，具体来说，在计算前向过程时，部分中间变量会被直接释放，等到反向过程时再进行重新计算。

举例来说，如果不进行 gradient checkpointing，每两个可学习操作之间的中间变量都需要被保存下来，用于计算梯度。当使用 gradient checkpointing 时，只有一些关键的中间变量被保存下来，其余的被丢弃。当进行反向传播时，所使用的中间变量需要从最近的 checkpoint 处重新执行一遍前向过程来计算得到。

如下图所示，在进行前向传播时，只有刻度所在的几个位置的中间变量被保存下来，当某个位置需要计算梯度时，需要重新从刻度的位置执行前向过程，计算出对应的中间变量值：

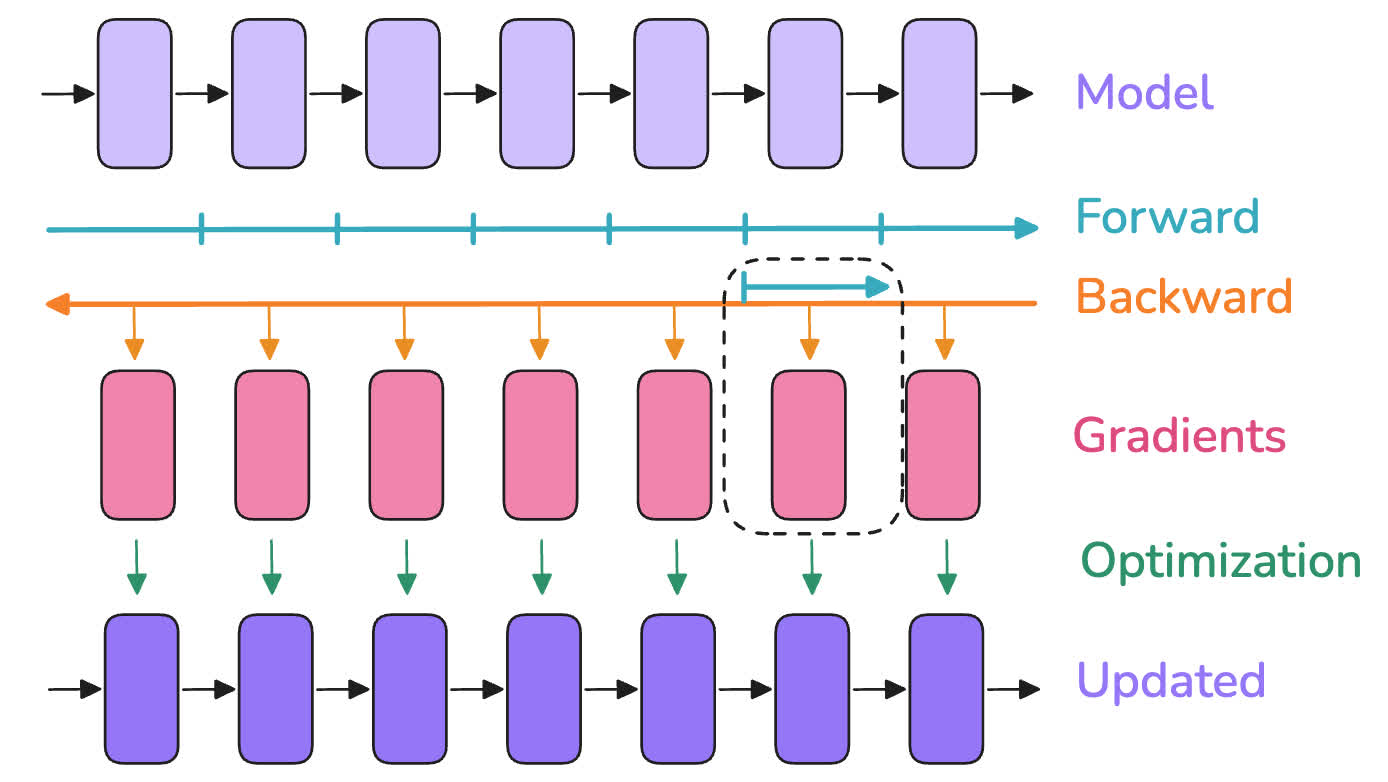
Gradient Checkpointing 示意图

在选择 checkpoint 的位置时，主要有以下两种策略：

  • 完全策略（Full）：在每两个 Transformer 层之间都进行 checkpoint，这种方式在反向传播时需要对每一层都重新进行一次前向传播，相当于每轮需要进行两次前向传播。这种策略最节省显存，但计算成本也非常高，基本会使计算成本增加 30-40%。
  • 选择性策略（Selective）：根据本论文的分析，比较好的 checkpoint 位置是在激活值增加最多、且计算开销最小的位置。根据这个标准，attention 的计算属于这一类，因此通常可以把 attention 的结果舍弃，而把开销大的结果保留。对于 GPT-3 175B 模型，这种策略可以在仅增加 2.7% 计算开销的前提下，节约 70% 的激活内存。

下面这张图展示了 gradient checkpointing 的使用对激活部分内存大小的影响。

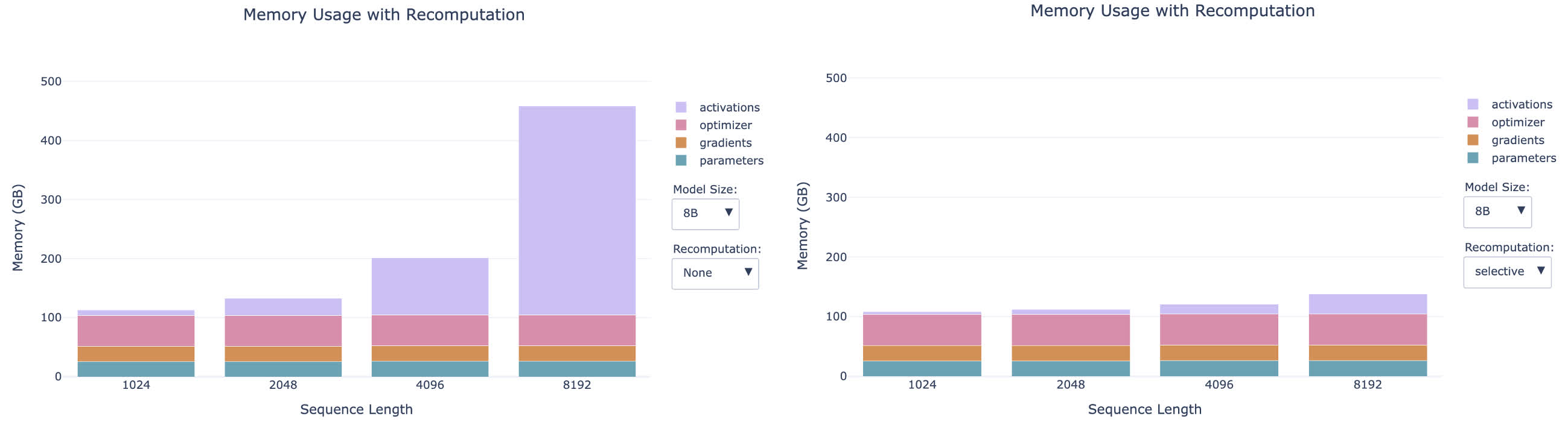
使用 Gradient Checkpointing 对显存的影响

通过 gradient checkpointing，可以节约大量的内存。由于访问内存通常比计算操作更慢，因此使用 gradient checkpointing 会使训练速度总体上加快。尽管如此，当 batch size 增加时，激活部分的内存仍然会线性地增加。为了解决这个问题，需要使用的技术是 gradient acumulation。

Gradient Accumulation

Gradient accumulation 也就是梯度累积，这种方法的思想很简单。对于一个 batch，这种方法将其拆分成多个小的 batch，然后再每个小 batch 上分别进行前向和反向传播，计算出梯度。最后，在进行优化操作之前，将所有的梯度计算均值。其中每次传播使用的 batch size 称为 micro-batch size，每次优化使用的所有 batch 的大小之和称为 global batch size。梯度累积的具体过程如下所示，可以发现每个 batch 需要进行多次前向和反向传播：

使用梯度累积时的训练过程

如果进一步思考，可以发现每个 micro-batch 的前向和反向过程都是相互独立的，因此可以拓展到多个 GPU。

梯度累积可以有效地增加 batch size（甚至可以增加到无穷大），同时保持显存占用不变。同时梯度累积也和 gradient checkpointing 可以同时使用，来进一步减少显存占用。当然梯度累积也有缺点，首先就是同一个 batch 需要拆分成多次进行计算；其次是由于需要将梯度累积起来，在第二次以及之后的每次前向传播时，所有的梯度均不能被释放，这会导致峰值内存升高。

这一部分的内容到这里就结束了，后续会继续学习一些并行化策略，敬请期待下一期学习笔记。