笔记|扩散模型(一八)Flow Matching 理论详解
在 Stable Diffusion 3 中,模型是通过 Flow Matching 的方法训练的。从这个方法的名字来看,就知道它和 Flow-based Model 有比较强的关联,因此在正式开始介绍这个方法之前先交代一些 Flow-based Model 相关的背景知识。
Flow-based Models
Normalizing Flow
Normalizing Flow 是一种基于变换对概率分布进行建模的模型,其通过一系列离散且可逆的变换实现任意分布与先验分布(例如标准高斯分布)之间的相互转换。在 Normalizing Flow 训练完成后,就可以直接从高斯分布中进行采样,并通过逆变换得到原始分布中的样本,实现生成的过程。(有关 Normalizing Flow 的详细理论介绍可以移步我的这篇文章观看)
从这个角度看,Normalizing Flow 和 Diffusion Model 是有一些相通的,其做法的对比如下表所示。从表中可以看到,两者大致的过程是非常类似的,尽管依然有些地方不一样,但这两者应该可以通过一定的方法得到一个比较统一的表示。
| 模型 | 前向过程 | 反向过程 |
|---|---|---|
| Normalizing Flow | 通过显式的可学习变换将样本分布变换为标准高斯分布 | 从标准高斯分布采样,并通过上述变换的逆变换得到生成的样本 |
| Diffusion Model | 通过不可学习的 schedule 对样本进行加噪,多次加噪变换为标准高斯分布 | 从标准高斯分布采样,通过模型隐式地学习反向过程的噪声,去噪得到生成样本 |
Continuous Normalizing Flow
Continuous Normalizing Flow(CNF),也就是连续标准化流,可以看作 Normalizing Flow 的一般形式。CNF 将原本 Normalizing Flow 中离散的变换替换为连续的变换,并用常微分方程(ODE)来表示,可以写成以下的形式: \[ \frac{\mathrm{d}\mathbf{z}_t}{\mathrm{d}t}=v(\mathbf{z}_t,t) \] 其中 \(t\in[0,1]\),\(\mathbf{z}_t\) 可以看作时间 \(t\) 下的数据点,\(v(\mathbf{z}_t,t)\) 是一个向量场,定义了数据点在每个时间下的变化大小与方向,这个向量场通常由神经网络来学习。当这个向量场完成了学习后,就可以用迭代法来求解: \[ \mathbf{z}_{t+\Delta t}=\mathbf{z}_t+\Delta t\cdot v(\mathbf{z}_t,t) \] 也就是说,一旦我们得知从标准高斯分布到目标分布的变换向量场,就可以从标准高斯分布采样,然后通过上述迭代过程得到目标分布中的一个近似解,完成生成的过程。这和离散的 Normalizing Flow 是一致的。
在 Normalizing Flow 中存在 Change of Variable Theory,这个定理是用来保证概率分布在进行变化时,概率密度在全体分布上的积分始终为 1 的一个式子(具体解释可以看上边给出的那篇 Normalizing Flow 的文章),其形式为: \[ p(\mathbf{x})=\pi(\mathbf{z})\left|\mathrm{det}\ \frac{\mathrm{d}\mathbf{z}}{\mathrm{d}\mathbf{x}}\right|=\pi(\mathbf{f}^{-1}(\mathbf{x}))\left|\mathrm{det}\ \mathbf{J}(\mathbf{f}^{-1}(\mathbf{x}))\right| \] 在 Flow Matching 的论文中,也给出了形式类似的公式,称为 push-forward equation,定义为: \[ p_t=[\phi_t]_*p_0 \] 其中的 push-forward 运算符,也就是星号,定义为: \[ [\phi_t]_*p_0(x)=p_0(\phi_t^{-1}(x))\mathrm{det}\left[\frac{\partial\phi_t^{-1}}{\partial x}(x)\right] \] 可以看出形式也是类似的。
连续性方程
概率分布在向量场中进行变换这一过程可以用物理学中的传输行为来建模。这是因为不管概率分布如何变换,其在全体分布上的积分始终为 1,因此可以认为概率密度也是一个守恒的物理量,可以类比物理学中的质量、电荷等的传输行为进行建模。这个建模方式就是连续性方程,其在物理学中定义如下: \[ \frac{\partial\rho}{\partial t}+\mathrm{div}(\rho\mathbf{v})=0 \] 其中 \(\rho\) 是流体的密度、\(\mathbf{v}\) 是流体的速度矢量、\(\frac{\partial\rho}{\partial t}\) 是流体密度随时间的变化率、\(\mathrm{div}(\rho\mathbf{v})\) 是质量通量密度的散度。这个方程的意义是:流体中任意封闭体积内的质量变化率等于流入流出该空间的流体质量流量之差。
类比到概率分布,这个方程可以写成: \[ \frac{\partial p_t(\mathbf{x})}{\partial t}+\mathrm{div}(p_t(\mathbf{x})v_t(\mathbf{x}))=0 \] 在上式中 \(p_t(\mathbf{x})\) 是 \(t\) 时刻对应的概率密度函数、\(v_t(\mathbf{x})\) 是与 \(p_t(\mathbf{x})\) 关联的向量场。这个式子是向量场 \(v_t(\mathbf{x})\) 能够产生概率密度路径 \(p_t(\mathbf{x})\) 的充分必要条件,在后续的推导中会用这个式子作为一个约束来使用。
在讲解 Score-based Model 的文章中,我们用随机微分方程(SDE)统一了 SMLD(Score Matching with Langevin Dynamics)和 DDPM,并且将 SDE 转化为了 ODE 概率流。也就是说,扩散模型同样能够用一个 ODE 来表示,因此,扩散模型也应当能够利用 CNF 的训练方式进行训练,这个训练的方式就是 Flow Matching。
Flow Matching
符号定义
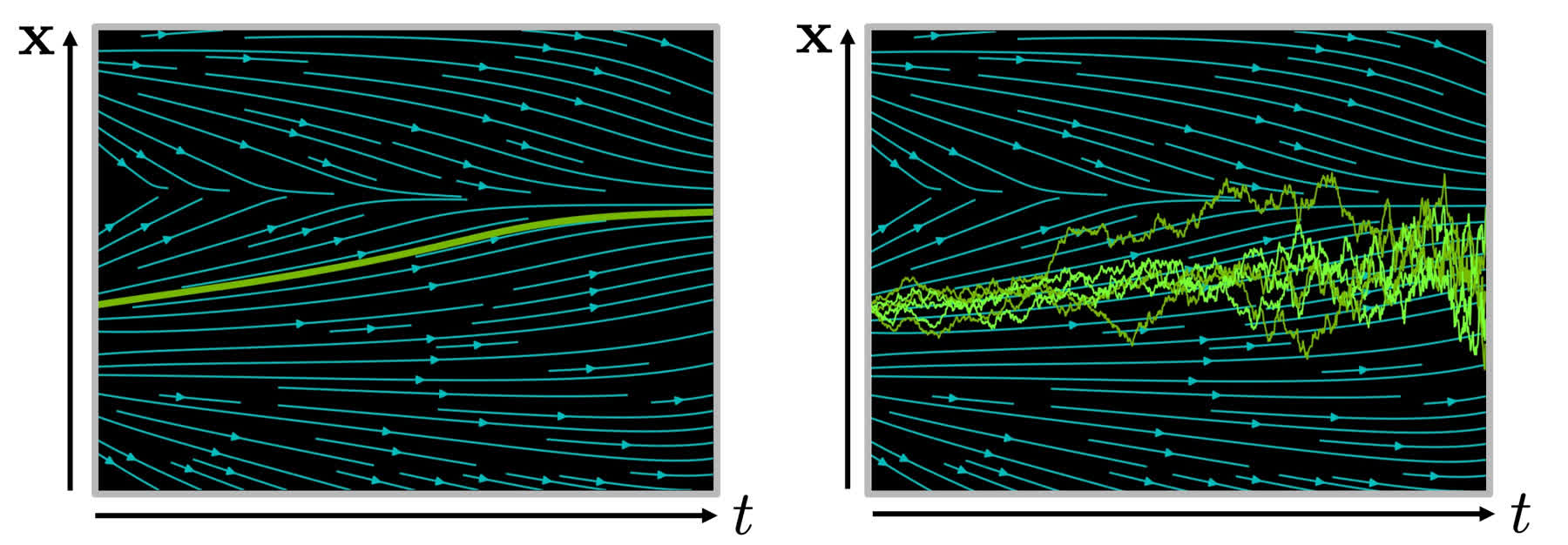
在正式开始介绍之前我们先介绍一下各个概念以及符号定义。借用一下之前介绍 SDE 时的一张图,如下所示。在 Flow Matching 中存在以下几个概念:
- 数据分布 \(p_0\)、\(p_t\)、\(p_1\):这个不用多解释,不过需要注意下标定义为 0 是标准高斯分布、1 是样本,这个定义和 DDPM 是相反的,需要注意
- Flow \(\phi_t\) 或 \(\psi_t\):这个也就是对分布进行变换的操作,例如 \(p_t=\phi_t(p_0)\)
- 向量场 \(v_t\):这个相当于下图中的青色箭头,样本沿着箭头的方向传输
- 概率路径 \(p_t\):这个相当于下图中的浅绿色曲线
在实际上进行训练时,神经网络建模的是向量场 \(v_t\),通过设定不同的 \(\phi_t\) 和 \(p_t\) 可以得到不同的 \(v_t\)。
概述
Flow Matching 的训练目标和 Score Matching 是比较类似的,学习的目标就是通过学习拟合一个向量场 \(u_t\),使得能够得到对分布进行变换的概率路径 \(p_t\),也就是下边这个公式: \[ \mathcal{L}_\mathrm{FM}(\theta)=\mathbb{E}_{t,p_t(x)}||v_t(x)-u_t(x)||^2 \] 其中 \(\theta\) 是模型的可训练参数,\(t\) 在 0 到 1 之间均匀分布,\(x\sim p_t(x)\) 是概率路径,\(v_t(x)\) 是由模型表示的向量场。这个训练目标的含义为:利用模型 \(\theta\) 来拟合一个向量场 \(u_t(x)\),使得最终通过学习到的 \(v_t(x)\) 可以得到概率路径 \(p_t(x)\),并且满足 \(p_1(x)\approx q(x)\)。
不过实际上这个公式并不实用,首先能够满足 \(p_1(x)\approx q(x)\) 的概率路径是很多的,其次我们也不知道 \(u_t(x)\) 究竟是什么东西,所以无法直接用来计算损失。本文主要证明了三个定理,用来构造上边这个损失的实用形式。
从条件概率路径和向量场构造
虽然我们不知道 \(p_t(x)\) 和 \(u_t(x)\) 的具体形式,但是我们可以通过添加条件将其转换为可以求得的形式(可以类比在 DDPM 推导时将 \(p(\mathbf{x}_{t-1}|\mathbf{x}_t)\) 转换为了 \(p(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0)\))。也就是说,虽然 \(u_t(x)\) 不知道,但是可以通过学习条件向量场 \(u_t(x|x_1)\),使得最后通过这个向量场能够生成条件概率路径 \(p_t(x|x_1)\)。第一个定理就是为了说明这个带条件的形式和不带条件的形式是等价的,也就是:
定理一:给定向量场 \(u_t(x|x_1)\),其能够生成条件概率路径 \(p_t(x|x_1)\),那么对于任意分布 \(q(x_1)\),满足某一特定形式(后文会给出)的边缘向量场 \(u_t(x)\) 就能生成对应的边缘概率路径 \(p_t(x)\)。
证明:首先,对于边缘概率路径 \(p_t(x)\),有以下等式: \[ p_t(x)=\int p_t(x|x_1)q(x_1)\mathrm{d}x_1 \] 进而可以推导: \[ \begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}p_t(x)&=\frac{\mathrm{d}}{\mathrm{d}t}\int p_t(x|x_1)q(x_1)\mathrm{d}x_1 \\ &=\int\frac{\mathrm{d}}{\mathrm{d}t}p_t(x|x_1)q(x_1)\mathrm{d}x_1&\mathrm{Leibniz~integral~rule} \\ &=-\int\mathrm{div}(u_t(x|x_1)p_t(x|x_1))q(x_1)\mathrm{d}x_1&\mathrm{Continuity~equation} \\ &=-\mathrm{div}\left(\int u_t(x|x_1)p_t(x|x_1)q(x_1)\mathrm{d}x_1\right)&\mathrm{Leibniz~integral~rule} \\ \end{aligned} \] 又根据连续性方程: \[ \frac{\mathrm{d}}{\mathrm{d}t}p_t(x)=-\mathrm{div}\left(u_t(x)p_t(x)\right) \] 两个式子联立得到 \(u_t(x)\) 需要满足以下形式: \[ u_t(x)=\int u_t(x|x_1)\frac{p_t(x|x_1)q(x_1)}{p_t(x)}\mathrm{d}x_1 \] 也就是说,只要 \(u_t(x)\) 满足上边等式中的形式,就可以用 \(u(x|x_1)\) 和 \(p(x|x_1)\) 取代 \(u(x)\) 和 \(p(x)\)。
Conditional Flow Matching
虽然基于上述过程已经推导出了 \(u_t(x)\) 的形式,但上述的积分依然不容易求解。因此作者给出了一种更容易求解的形式(如下所示),并且证明了下面这个损失函数与原本损失函数的等价性。 \[ \mathcal{L}_\mathrm{CFM}(\theta)=\mathbb{E}_{t,q(x_1),p_t(x|x_1)}||v_t(x)-u_t(x|x_1)||^2 \] 作者证明了 \(\mathcal{L}_{CFM}\) 和 \(\mathcal{L}_{FM}\) 的等价性,也就是说优化 \(\mathcal{L}_{CFM}\) 等价于优化 \(\mathcal{L}_{FM}\):
定理二:假定对于所有 \(x\in\mathbb{R}^d\) 且 \(t\in[0,1]\) 都有 \(p_t(x)>0\),那么 \(\mathcal{L}_{CFM}\) 和 \(\mathcal{L}_\mathrm{FM}\) 相差一个与 \(\theta\) 无关的常数,即有 \(\nabla_\theta\mathcal{L}_\mathrm{FM}(\theta)=\nabla_\theta\mathcal{L}_\mathrm{CFM}(\theta)\)。
证明:首先把两个二次项都展开,然后证明右侧是相等的。注意,虽然右侧都有 \(\left\Vert v_t(x)\right\Vert^2\) 这一项,但由于 \(\mathbb{E}\) 的下标不一样,所以不能直接认为两者相等。 \[ \begin{align} \left\Vert v_t(x)-u_t(x)\right\Vert^2&=\left\Vert v_t(x)\right\Vert^2-2\left\langle v_t(x),u_t(x)\right\rangle+\left\Vert u_t(x)\right\Vert^2 \\ \left\Vert v_t(x)-u_t(x|x_1)\right\Vert^2&=\left\Vert v_t(x)\right\Vert^2-2\left\langle v_t(x),u_t(x|x_1)\right\rangle+\left\Vert u_t(x|x_1)\right\Vert^2 \end{align} \] 由于 \(u_t\) 相当于 groundtruth,和 \(\theta\) 无关,所以不产生梯度,在计算时可以直接略去最后一项。分别证明前两项相等: \[ \begin{aligned} \mathbb{E}_{p_t(x)}\left\Vert v_t(x)\right\Vert^2&=\int\left\Vert v_t(x)\right\Vert^2p_t(x)\mathrm{d}x \\ &=\int\left\Vert v_t(x)\right\Vert^2p_t(x|x_1)q(x_1)\mathrm{d}x_1\mathrm{d}x \\ &=\mathbb{E}_{q(x_1),p_t(x|x_1)}\left\Vert v_t(x)\right\Vert^2 \end{aligned} \]
\[ \begin{aligned} \mathbb{E}_{p_t(x)}&=\int\left\langle v_t(x),\frac{\int u_t(x|x_1)p_t(x|x_1)q(x_1)\mathrm{d}x_1}{p_t(x)}\right\rangle p_t(x)\mathrm{d}x \\ &=\int\left\langle v_t(x),\int u_t(x|x_1)p_t(x|x_1)q(x_1)\mathrm{d}x_1\right\rangle\mathrm{d}x \\ &=\int\left\langle v_t(x),u_t(x|x_1)\right\rangle p_t(x|x_1)q(x_1)\mathrm{d}x_1\mathrm{d}x \\ &=\mathbb{E}_{q(x_1),p_t(x|x_1)}\left\langle v_t(x),u_t(x|x_1)\right\rangle \end{aligned} \]
如此即证明了上述的定理。这样,我们的训练就不再依赖于一个抽象的边缘向量场,而是依赖于 \(x_1\) 的条件向量场。这样我们就可以利用一定的训练数据对模型进行训练。
条件概率路径和向量场
上面我们已经证明了条件概率路径和条件向量场可以等价于边缘概率路径和边缘向量场,并且用 CFM 的方式进行训练和 Flow Matching 的效果是相同的。但现在 \(u_t(x|x_1)\) 的形式依然是不知道的,因此我们需要进一步定义具体的条件概率路径的形式。就像 DDPM,我们需要定义具体的前向过程,才能基于这个过程进行训练。
作者给出的条件概率路径的形式为: \[ p_t(x|x_1)=\mathcal{N}(x|\mu_t(x_1),\sigma_t(x_1)^2I) \] 其中 \(\mu\) 是和时间有关的高斯分布均值,\(\sigma\) 是和时间有关的高斯分布方差。并且为了使这个条件概率路径有比较良好的性质,作者设定在 \(t=0\) 时 \(p(x)\) 为标准高斯分布 \(\mathcal{N}(x|0,I)\),也就是 \(\mu_0(x_1)=0\)、\(\sigma_0(x_1)=1\);同时希望条件概率路径最终能够生成目标样本,所以当 \(t=1\) 时高斯分布的均值和方差 \(\mu_1(x_1)=x_1\)、\(\sigma_1(x_1)=\sigma_\min\),其中 \(\sigma_\min\) 时一个足够小的数。
同时,作者将 flow 定义为以下形式: \[ \psi_t(x)=\sigma_t(x_1)x+\mu_t(x_1) \] 其中 \(x\sim\mathcal{N}(0,I)\) 服从标准高斯分布,根据上文所述的 CNF 的 ODE 表示,有: \[ \frac{\mathrm{d}}{\mathrm{d}t}\psi_t(x)=u_t(\psi_t(x)|x_1) \] 这样我们就可以将损失函数 \(\mathcal{L}_\mathrm{CFM}\) 的形式变为如下形式: \[ \mathcal{L}_\mathrm{CFM}(\theta)=\mathbb{E}_{t,q(x_1),p(x_0)}\left\Vert v_t(\psi_t(x_0))-\frac{\mathrm{d}}{\mathrm{d}t}\psi_t(x_0)\right\Vert^2 \] 在上边的式子里,\(\psi_t\) 的形式是已知的,并且 \(x_0\sim\mathcal{N}(0,I)\),所以上边的式子是可以求解的,是实用、可以实现的损失函数。同时,也可以得到条件向量场的形式,即:
定理三:令 \(p_t(x|x_1)\) 是上述的高斯概率路径,\(\psi_t\) 是上述的 flow map,那么 \(\psi_t(x)\) 对应于唯一的向量场 \(u_t(x|x_1)\),且形式为: \[ u(x|x_1)=\frac{\sigma'_t(x_1)}{\sigma_t(x_1)}(x-\mu(x_1))+\mu'_t(x_1) \] 证明:由于 \(\psi_t\) 可逆,令 \(x=\psi^{-1}(y)\),则可以写出: \[ \psi^{-1}(y)=\frac{y-\mu_t(x_1)}{\sigma_t(x_1)} \] 同时对 \(\psi_t\) 求导得到: \[ \psi'_t(x)=\sigma'_t(x_1)x+\mu'_t(x_1) \] 根据 ODE,推导得到: \[ \begin{aligned} u_t(y|x_1)&=\psi'_t(x)=\psi'_t(\psi_t^{-1}(y))=\psi'_t(\sigma'_t(x_1)y+\mu'_t(x_1)) \\ &=\frac{\sigma'_t(x_1)}{\sigma_t(x_1)}(y-\mu_t(x_1))+\mu'_t(x_1) \end{aligned} \]
讨论
Flow Matching 定义了一种特定形式的高斯概率路径,当选择不同的均值和方差时,有几种特殊的情况:
- Variance Exploding: \(p_t(x)=\mathcal{N}(x|x_1,\sigma_{1-t}^2I)\),其中 \(\mu_t(x_1)=x_1\)、\(\sigma_t(x_1)=\sigma_{1-t}\),并且 \(\sigma_t\) 是递增函数,\(\sigma_0=0\)、\(\sigma_1\gg1\)。这种过程能够使模型生成数据时探索范围更广的空间,有助于生成多样的样本。
- Variance Preserving: \(p_t(x|x_1)=\mathcal{N}(x|\alpha_{1-t}x_1,(1-\alpha_{1-t}^2)I)\),其中 \(\mu_t(x_1)=\alpha_{1-t}x_1\)、\(\sigma_t(x_1)=\sqrt{1-\alpha_{1-t}^2}\)。这种过程在引入噪声的同时保持整体方差不变,这样能使数据的分布比较稳定。(可以看出 DDPM 就是这种过程)
- Optimal Transport Conditional: 定义均值和方差为 \(\mu_t(x)=tx_1\)、\(\sigma_t(x)=1-(1-\sigma_\min)t\)。可以求得最优传输路径是直线,因此可以更快地训练和采样。(这个比较类似于 Rectified Flow)
总结
Flow Matching 的确理论性比较强,不是特别好理解。概括来说主要是给出了一种用来训练 CNF 的方法,并且提出了三个定理分别用来解决 flow 的表示问题、loss 函数的设计问题以及具体实现方式的问题。同时 flow matching 也统一了 score matching 和 DDPM,非常巧妙。(学到这里终于快要把 stable diffusion 3 的拼图拼完了,真不容易)
参考资料: