论文链接：Progressive Distillation for Fast Sampling of Diffusion Models

近期在研究 Rectified Flow 时发现 diffusers 中一个相关的 PR（#5397）训练用到了 Velocity Prediction，回想起之前某次面试还被问到了这个问题，决定来学习一下这究竟是什么东西。

对 CompVis 实现的 Stable Diffusion 代码比较熟悉的读者应该或多或少都在 scheduler 中读到过这样一段代码：

if self.parameterization == "eps":
    target = noise
elif self.parameterization == "x0":
    target = x_start
elif self.parameterization == "v":
    target = self.get_v(x_start, noise, t)

这是在计算损失时，也就是 p_loss 函数中的几种不同的计算方式。前两种应该比较简单，"eps" 是预测噪声，"x0" 是预测原图；最后一种就是这里要讲的预测 velocity。观察一下这个 get_v 函数：

def get_v(self, x, noise, t):
    return (
        extract_into_tensor(self.sqrt_alphas_cumprod, t, x.shape) * noise -
        extract_into_tensor(self.sqrt_one_minus_alphas_cumprod, t, x.shape) * x
    )

可以看出这里的 velocity 是 x0 和 eps 的加权求和。下面我们会推导这样做的依据。

Velocity Prediction

这个方法是在文章开头给出的论文中提出的，文中给出的扩散模型的预测目标为：

\[ \mathbf{v}\equiv\alpha_t\epsilon-\sigma_t\mathbf{x} \]

并且在预测后可以通过以下公式得到 \(\hat{\mathbf{x}}\)：

\[ \hat{\mathbf{x}}=\alpha_t\mathbf{z}_t-\sigma_t\hat{\mathbf{v}_\theta}(\mathbf{z}_t) \]

要理解上述结论，需要参考一下原论文中的这张图：

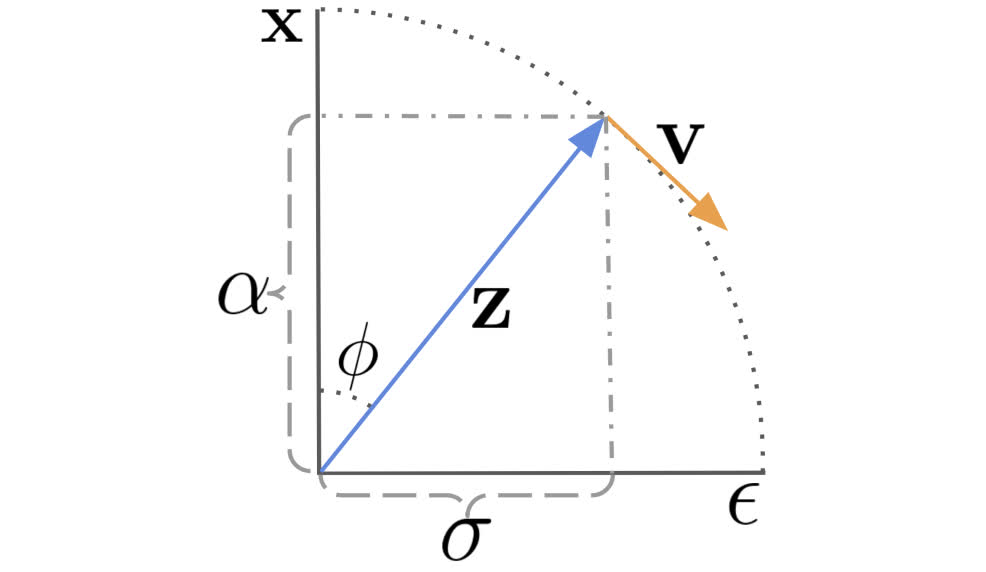
Velocity Prediction 的示意图

在 DDPM 中，加噪过程的公式为：

\[ \mathbf{x}_t=\sqrt{\bar{\alpha}_t}\mathbf{x}_0+\sqrt{1-\bar{\alpha}_t}\epsilon \]

可以看出 \(\mathbf{x}_0\) 和 \(\epsilon\) 的系数平方和为 1，因此可以把两个系数看作单位圆的半径在两条坐标轴上投影的长度，假定这条半径与坐标轴的夹角为 \(\phi\)，上式中的两个系数就可以分别写成 \(\cos\phi\) 和 \(\sin\phi\)。

在正式开始推导之前先统一一下符号，在这篇论文里，DDPM 的加噪公式被写成：

\[ \mathbf{x}_t=\alpha_t\mathbf{x}+\sigma_t\epsilon \]

也就是说，这里的 \(\alpha_t\) 相当于 DDPM 中的 \(\sqrt{\bar{\alpha}_t}\)、\(\mathbf{x}\) 相当于 DDPM 中的 \(\mathbf{x}_0\)，而这里的 \(\sigma_t\) 则相当于 DDPM 中的 \(\sqrt{1-\bar{\alpha}_t}\)，这在上图中也有体现。同时，根据图中的定义，\(\alpha_t=\cos\phi\)、\(\sigma_t=\sin\phi\)。从图中可以看出，速度 \(\mathbf{v}\) 被定义为这条半径的切线方向，也就是 \(\mathbf{z}\) 关于 \(\phi\) 的导数：

\[ \begin{aligned} \mathbf{v}&\equiv\frac{\mathrm{d}\mathbf{z}}{\mathrm{d}\phi}=\frac{\mathrm{d}\cos\phi}{\mathrm{d}\phi}\mathbf{x}+\frac{\mathrm{d}\sin\phi}{\mathrm{d}\phi}\epsilon=\cos(\phi)\epsilon-\sin(\phi)\mathbf{x}\\ &=\alpha_t\epsilon-\sigma_t\mathbf{x} \end{aligned} \]

为了得到推理阶段的表达式，可以将这个式子与上边的加噪公式联立消掉 \(\epsilon\)：

\[ \begin{cases} \begin{aligned} \mathbf{x}_t&=\alpha_t\mathbf{x}+\sigma_t\epsilon\\ \mathbf{v}&=\alpha_t\epsilon-\sigma_t\mathbf{x} \end{aligned} \end{cases} \]

直接消元，利用 \(\alpha_t^2+\sigma_t^2=1\) 即可得到 \(\hat{\mathbf{x}}\) 的表达式：

\[ \hat{\mathbf{x}}=\alpha_t\mathbf{z}_t-\sigma_t\hat{\mathbf{v}_\theta}(\mathbf{z}_t) \]

这样我们就得到了预测 velocity 时的推理公式。下面我们再来梳理一下训练和推理的过程：

在训练阶段，依然是用 DDPM 的方式给原图加噪，不过模型的预测目标是 \(\mathbf{v}\)，并且用上边的公式计算出的结果监督；
在推理阶段，模型预测出速度 \(\mathbf{v}\)，可以用上边的 \(\hat{\mathbf{x}}\) 的表达式计算出预测的原图，之后的流程就和其他的相同了（也就是先和 \(\mathbf{x}_t\) 加权求出 \(\mathbf{x}_{t-1}\) 再继续去噪）。

直观理解

从速度 \(\mathbf{v}\) 的表达式来看，它是原图 \(\mathbf{x}_0\) 和噪声 \(\epsilon\) 的加权求和，因此可以把对速度的预测看作介于直接预测原图和直接预测噪声中间的一个预测目标。

原论文之所以要这样做，是因为预测 \(\epsilon\) 相当于预测原图与信噪比 \(\mathrm{SNR}(t)\) 的乘积，当 \(t\rightarrow1\) 时这个预测与原图无关。在普通的 DDPM 中，由于采样次数足够多，在后续的步骤中这个问题会被修正，但由于这篇文章要通过蒸馏减少采样步骤数量，所以会受到这个问题的影响。因此使用速度预测，即使在第一步也能有原图的部分信息作为引导，能够改善这个问题。

参考资料：

扩散模型中的v-prediction推导