笔记|扩散模型(五)Classifier-Free Guidance 理论与实现
上一篇文章我们学习了 Classifier Guidance,这种方法通过引入一个额外的分类器,使用梯度引导的方式成功地实现了条件生成。虽然 Classifier Guidance 可以直接复用训练好的 diffusion models,不过这种方法的问题是很明显的,首先需要额外训练一个分类器,而且这个分类器不仅仅分类一般的图像,还需要分类加噪后的图像,这会给方法带来比较大的额外开销;其次分类器训练完成后类别就固定下来了,如果希望生成新的类别就需要重新训练分类器。这篇文章学习的 Classifier-Free Guidance 则可以比较好地解决这些问题。
Classifier-Free Guidance
在 Classifier Guidance 中,从条件概率 \(p(\mathbf{x}_t|y)\) 出发,利用贝叶斯公式和 score function 推导出了以下公式,在下面的公式中,等号右侧的第一项已知,第二项则需要引入分类器进行计算。 \[ \nabla_{\mathbf{x}_t}\log p(\mathbf{x}_t|y)=\underbrace{\nabla_{\mathbf{x}_t}\log p(\mathbf{x}_t)}_{\textrm{unconditional}~\textrm{score}}+\underbrace{\nabla_{\mathbf{x}_t}\log p(y|\mathbf{x}_t)}_{\textrm{adversarial}~\textrm{gradient}} \] 并且在实际使用时,为了调节控制的强度,会引入一个额外的叫做 guidance scale 的参数 \(s\)。最终的结果是以 \(s\) 作为权重进行加权的结果,也就是: \[ \nabla_{\mathbf{x}_t}\log p(\mathbf{x}_t|y)=\nabla_{\mathbf{x}_t}\log p(\mathbf{x}_t)+s\nabla_{\mathbf{x}_t}\log p(y|\mathbf{x}_t) \] 现在我们不希望使用分类器来计算 \(\nabla_{\mathbf{x}_t}\log p(y|\mathbf{x}_t)\) 这一项,因此需要用另一种方式来表示这一项,把第一个公式中的这一项移到等号左侧: \[ \nabla_{\mathbf{x}_t}\log p(y|\mathbf{x}_t)=\nabla_{\mathbf{x}_t}\log p(\mathbf{x}_t|y)-\nabla_{\mathbf{x}_t}\log p(\mathbf{x}_t) \] 然后再代入第二个含有参数 \(s\) 的公式: \[ \begin{aligned} \nabla_{\mathbf{x}_t}\log p(\mathbf{x}_t|y)&=\nabla_{\mathbf{x}_t}\log p(\mathbf{x}_t)+s\nabla_{\mathbf{x}_t}\log p(y|\mathbf{x}_t)\\ &=\nabla_{\mathbf{x}_t}\log p(\mathbf{x}_t)+s\left(\nabla_{\mathbf{x}_t}\log p(\mathbf{x}_t|y)-\nabla_{\mathbf{x}_t}\log p(\mathbf{x}_t)\right)\\ &=\underbrace{(1-s)\nabla_{\mathbf{x}_t}\log p(\mathbf{x}_t)}_{\textrm{unconditional}~\textrm{score}}+\underbrace{s\nabla_{\mathbf{x}_t}\log p(\mathbf{x}_t|y)}_{\textrm{conditional}~\textrm{score}} \end{aligned} \] 到这一步就已经得到 classifier-free guidance 的形式了。在上边的式子里第一项对应于无条件生成的分数,第二项对应于有条件生成的分数,\(s\) 是一个用来控制条件重要性的参数,当 \(s=0\),模型就是原来的无条件生成模型;当 \(s=1\),模型完全依赖于条件;当 \(s>1\),模型不仅更加重视条件,而且向远离无条件生成的方向移动。一般来说参数的取值为 \(s=7.5\),之所以不在 0 到 1 之间取值是因为我们想生成的并不是介于「无条件生成」和「有条件生成」之间的一种似是而非的样本,而是非常明确符合条件的结果,因此这个参数的取值是比较大的。
上边的公式也可以写成另一种形式,如下所示。两项分别是无条件生成的分数以及从无条件生成指向有条件生成的方向,这样看就更清晰了:classifier-free guidance 就是从无条件生成的基础上向某个条件的方向移动。 \[ \nabla_{\mathbf{x}_t}\log p(\mathbf{x}_t|y)=\underbrace{\nabla_{\mathbf{x}_t}\log p(\mathbf{x}_t)}_{\textrm{unconditional}~\textrm{score}}+\underbrace{s(\nabla_{\mathbf{x}_t}\log p(\mathbf{x}_t|y)-\nabla_{\mathbf{x}_t}\log p(\mathbf{x}_t))}_{\textrm{unconditional}~\textrm{to}~\textrm{conditional}} \] 不过这个方法也有一些不容易理解的地方,观察一下公式可以发现 \(\nabla_{\mathbf{x}_t}\log p(\mathbf{x}_t|y)\) 这一项同时出现在了等式的左侧和右侧,那么如果想学习 \(\nabla_{\mathbf{x}_t}\log p(\mathbf{x}_t|y)\),直接对这一项进行学习就可以了,为什么还需要拆分成无条件生成和有条件生成两部分呢?根据我个人的理解,从上边的式子可以看出无条件生成是有条件生成的基础,生成的质量和多样性是由无条件生成的分数保证的,如果只有有条件生成而没有无条件生成,那么生成效果可能不佳。
训练与采样过程
从上一节我们已经知道了可以通过分别对无条件生成和有条件生成进行学习,得到无需分类器的有条件生成模型。那么需要学习的有两种模型,具体来说就是一个只输入带噪声图像的模型 \(\epsilon_\theta(\mathbf{x})\) 和一个同时输入噪声图和条件的模型 \(\epsilon_\theta(\mathbf{x},\mathbf{c})\)。不过原始论文的作者并没有这样做,因为使用两个模型的参数量比较大,并且实现比较复杂。要实现无条件生成,不一定要去掉额外的条件输入,直接把条件输入替换成某个固定的空值 \(\varnothing\) (例如 0)也是可以的。这样,有条件和无条件就被统一成了同一个模型 \(\epsilon_\theta(\mathbf{x},\mathbf{c})\),当 \(\mathbf{c}=\varnothing\) 就是无条件的情况。
为了联合训练有条件和无条件的情况,在训练时需要以一定的概率 \(p_\mathrm{uncond}\) 将条件输入替换为 \(\varnothing\)。其他的部分和一般的 diffusion model 的训练过程区别不大,论文中也给出了训练的算法,可以看到除了多了条件作为输入以及采样无条件生成的输入之外,没有其他的变化:

文中也给出了采样算法的流程,可以看到预测噪声由无条件和有条件两部分加权得到:

条件注入的方式
根据我们前文中的讨论,只需要给噪声预测模型加入一个条件参数,即可实现有条件去噪和无条件去噪。我们知道去噪模型通常使用的都是 UNet,将条件注入 UNet 有几种比较常见的方式,即交叉注意力、通道注意力以及自适应归一化等。
Cross Attention
交叉注意力是比较常用的一种条件注入方式,例如很多文生图模型的文本就是用这种方式注入的。在注入时是以
\(\mathbf{x}\) 为 query、以 \(\mathbf{c}\) 为 key 和
value。可以以下面这张图中的结构做为参考看一下 diffusers
的代码。
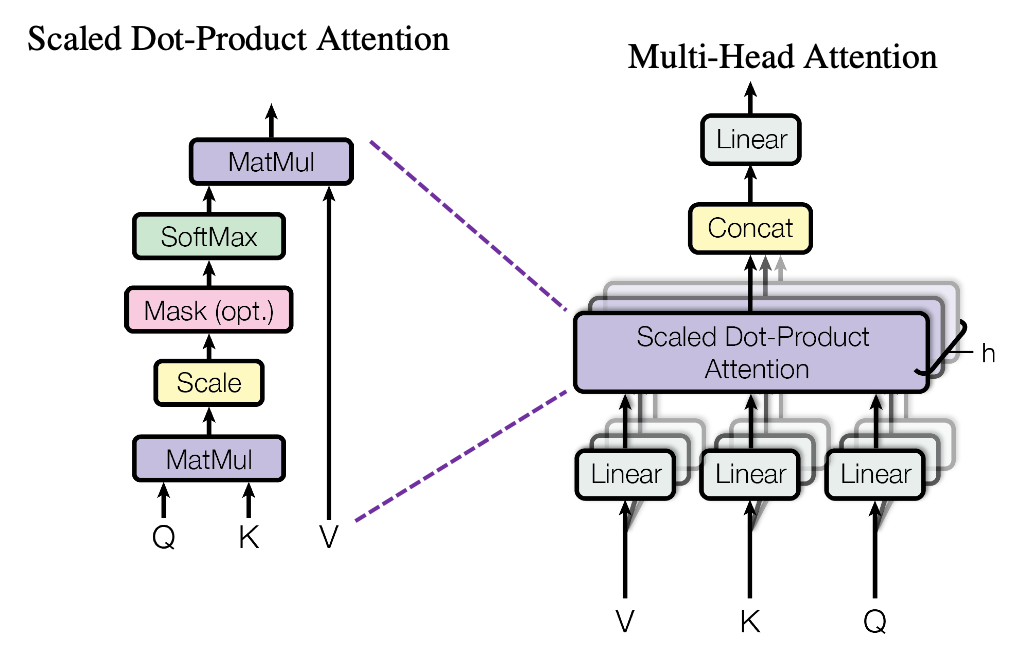
diffusers 对 UNet 中使用的 attention
进行了多层封装,具体的层次结构如下所示:
1 | diffusers.models.unets.unet_2d_condition.UNet2DConditionModel |
在上述层次关系中,我们只需要关心最后两层,也就是 attention 的具体实现。我们把其中核心的代码拿出来看:
1 | class Attention(nn.Module): |
可以看到直接调用了
processor,那么我们再看这个类是怎么实现的,具体的解释可以直接看注释:
1 | class AttnProcessor2_0: # 这个类实现了 scaled dot-product attention |
Channel-wise Attention
相比于交叉注意力,通道注意力相对比较简单。虽然叫注意力,但其实就是做完
projection 直接加到 time embedding 上,具体的代码可以参考
diffusers.models.embeddings.TimestepEmbedding:
1 | class TimestepEmbedding(nn.Module): |
上述代码中的 cond_proj 的定义如下,可以看到就是一个
linear 层:
1 | self.cond_proj = nn.Linear(cond_proj_dim, in_channels, bias=False) |
这种注入方式一般用于比较简单的条件的注入,例如类别条件等。
Adaptive Normalization
自适应归一化有几种,比如自适应层归一化、自适应组归一化以及一些变体。这里以最简单的情况为例,在
diffusers 中的实现位于
diffusers.models.normalization.AdaLayerNorm,可以看到是利用
timestep 对 x 进行了一个 affine 操作:
1 | class AdaLayerNorm(nn.Module): |
总体上来说,注入条件的方式还是很多的,可以根据条件的不同灵活地选择。关于这一部分在 DiT 中应该还会有更加详细的讨论,这里就不过多展开了。
采样过程的代码实现
在上一节中我们解决了如何将条件注入 UNet 的问题,现在我们可以直接认为 UNet 可以同时接收噪声图、时间步和条件三个输入。同时因为无条件生成与有条件生成的同时存在,UNet 也需要将输出的通道数变为 6,前三个通道表示无条件生成、后三个通道表示有条件生成,类似于 Improved DDPM。一个示意性的代码如下:
1 | for timestep in tqdm(scheduler.timesteps): |
总结
到这里关于 diffusion models 的理论性比较强的部分就暂时告一段落了,之后的内容会更加偏向应用。不得不说研究 diffusion models 对数学的要求还是挺高的,想出来这些方法的人们也真是够神仙)
参考资料: