笔记|Score-based Generative Models(二)基于 SDE 的模型
上一篇文章中我们介绍了 score-based model 的基本概念,包括其如何对分布进行建模、如何从建模的分布中进行采样以及通过对分布进行扰动提高其建模精度的方式。在这篇文章中我们将介绍的是如何使用随机微分方程(也就是 SDE)进行 score-based 建模。
随机微分方程简介
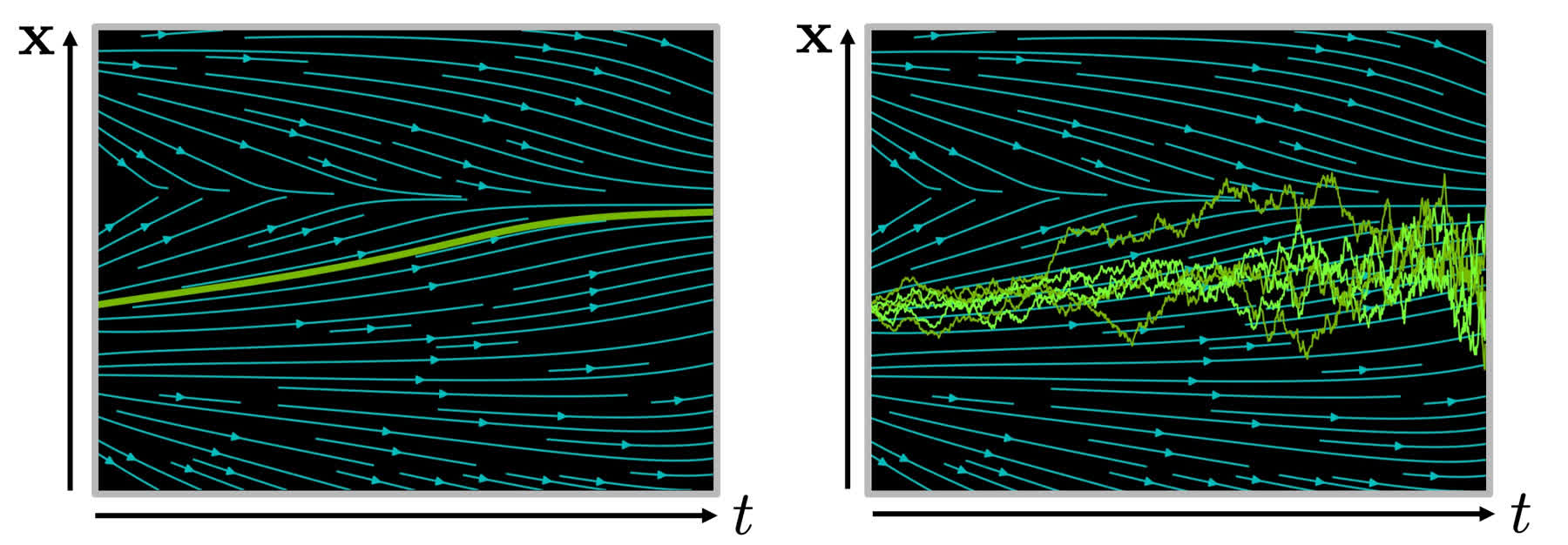
首先我们先介绍一些随机微分方程的基本知识以便理解。 我们首先举一个常微分方程(ODE)的例子,例如下面的一个常微分方程: \[ \frac{\mathrm{d}\mathbf{x}}{\mathrm{d}t}=\mathbf{f}(\mathbf{x},t)\quad\mathrm{or}\quad\mathrm{d}\mathbf{x}=\mathbf{f}(\mathbf{x},t)\mathrm{d}t \] 其中的 \(\mathbf{f}(\mathbf{x},t)\) 是一个关于 \(\mathbf{x}\) 和 \(t\) 的函数,其描述了 \(\mathrm{x}\) 随时间的变化趋势,如下面图中的左图所示。直观地说,\(\mathbf{f}(\mathbf{x},t)\) 对应于图中的青色箭头,确定了某一个时刻的 \(\mathbf{x}(t)\) 后,只要跟着箭头走就可以找到下一个时刻的 \(\mathbf{x}(t+\Delta t)\)。这个常微分方程可以得到解析解: \[ \mathbf{x}(t)=\mathbf{x}(0)+\int_0^t\mathbf{f}(\mathbf{x},\tau)\mathrm{d}\tau \] 然而在实际应用中我们使用的 \(\mathbf{f}(\mathbf{x},t)\) 通常是一个比较复杂的函数,例如神经网络,那么求出这个解析解显然是不现实的。因此,在实际应用时通常会用迭代法得到数值解: \[ \mathbf{x}(t+\Delta t)\approx\mathbf{x}(t)+\mathbf{f}(\mathbf{x}(t),t)\Delta t \] 在迭代过程中每次沿着箭头线性地走一小段距离,经过多次迭代就可以得到解析解的一个近似,这个迭代的过程可以用下面左图中的绿色曲线表示。
从上面的描述可以发现,常微分方程描述了一个确定性的过程,而对于非确定性的过程(比如从分布中采样),则需要使用随机微分方程(SDE)进行描述。随机微分方程相比于常微分方程只是在形式上多了一个高斯噪声: \[ \frac{\mathrm{d}\mathbf{x}}{\mathrm{d}t}=\underbrace{\mathbf{f}(\mathbf{x},t)}_{漂移系数}+\underbrace{\sigma(\mathbf{x},t)}_{扩散系数}\omega_t\quad\mathrm{or}\quad\mathrm{d}\mathbf{x}=\mathbf{f}(\mathbf{x},t)\mathrm{d}t+\sigma(\mathbf{x},t)\mathrm{d}\omega_t \] 在采样时和 ODE 类似,也可以进行迭代采样: \[ \mathbf{x}(t+\Delta t)\approx\mathbf{x}(t)+\mathbf{f}(\mathbf{x}(t),t)\Delta t+\sigma(\mathbf{x}(t),t)\sqrt{\Delta t}\mathcal{N}(0,I) \] 而且由于采样过程中存在高斯噪声,进行多次采样会得到不同的轨迹,如下边右图中的一系列绿色折线所示。
基于 SDE 的 Score-based Models
我们在上一篇文章介绍过,通过使用多个具有不同方差的高斯噪声对分布进行扰动,可以提升概率建模的质量。那么如果将噪声的方差数量推广到无穷大,也就是使用连续的方差对分布进行扰动,就可以进一步提高概率建模的准确度。
使用 SDE 描述扰动过程
当噪声的尺度数量接近无穷大的时候,扰动的过程类似于一个连续时间内的随机过程,如下图所示,可以看出这和扩散模型的加噪过程有一些类似之处。
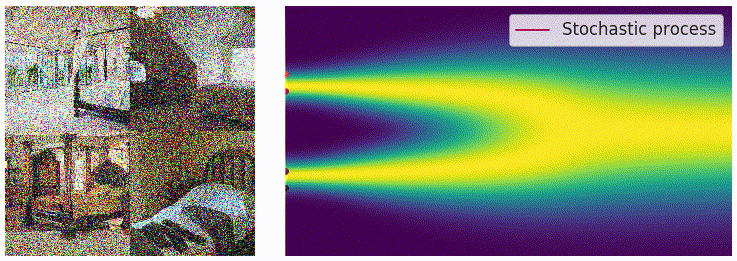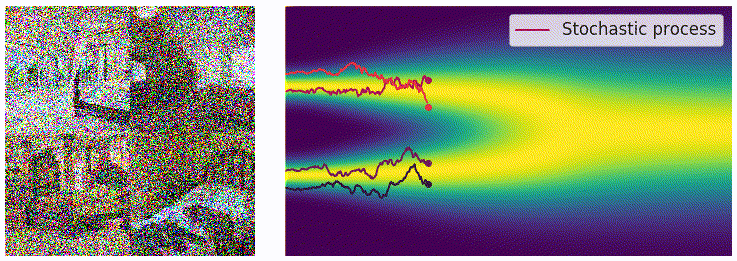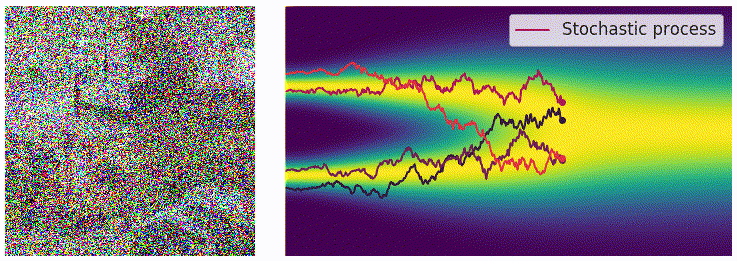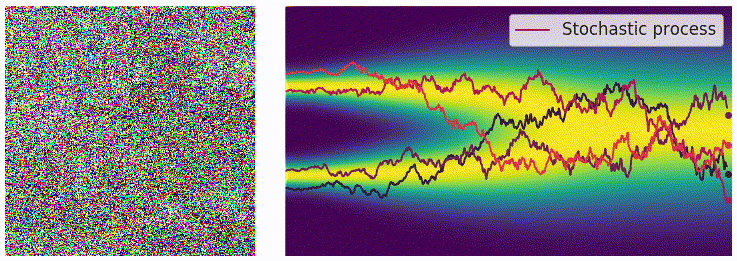
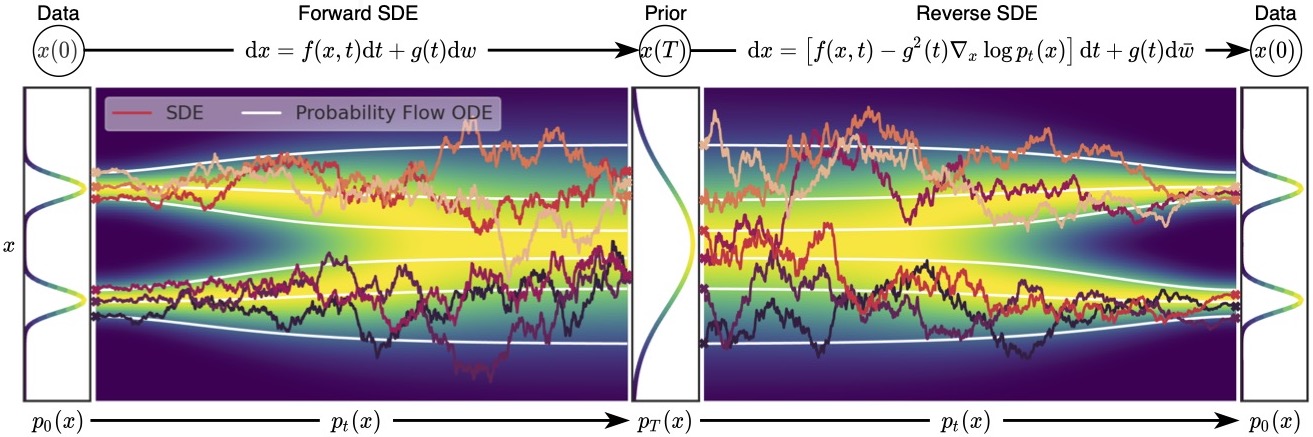
为了表示上述随机过程,可以用随机微分方程进行描述,和上面描述过的类似: \[ \mathrm{d}\mathbf{x}=\mathbf{f}(\mathbf{x},t)\mathrm{d}t+g(t)\mathrm{d}\mathbf{w} \] 用 \(p_t(\mathbf{x})\) 表示 \(\mathbf{x}(t)\) 的概率密度函数,可以知道 \(p_0(\mathbf{x})=p(\mathbf{x})\) 是没有加噪时的分布,也就是真实的数据分布,经过足够多个时间步 \(T\) 的扰动,\(p_T(\mathbf{x})\) 接近于先验分布 \(\pi(\mathbf{x})\)。从这个角度来说,扰动的过程和扩散模型的扩散过程是一致的。就像扩散模型可以使用很多种加噪 schedule,这个扰动的随机过程可以使用的 SDE 的形式也并不是唯一的,例如: \[ \mathrm{d}\mathbf{x}=e^t\mathrm{d}\mathbf{w} \] 就是用均值为 0、方差呈指数增长的高斯噪声对分布进行扰动。
使用反向 SDE 进行采样
在离散的过程里,可以用 annealed Langevin dynamics 进行采样,那么在这里我们的正向过程改为了使用 SDE 进行描述,逆向过程也要发生相应的变化。对于一个 SDE 来说,其逆向过程同样也是一个 SDE(推导过程见这个链接),可以表示为: \[ \mathrm{d}\mathbf{x}=\left[\mathbf{f}(\mathbf{x},t)-g^2(t)\textcolor{red}{\nabla_\mathbf{x}\log p_t(\mathbf{x})}\right]\mathrm{d}t+g(t)\mathrm{d}\mathbf{w} \] 这里的 \(\mathrm{d}t\) 表示的是反向的时间梯度,也就是从 \(t=T\) 到 \(t=0\) 的方向。上面的式子里有一部分我们非常熟悉,也就是红色的部分,正好就是我们上一篇文章中介绍的 score function \(\mathbf{s}_\theta(\mathbf{x},t)\)。从这里我们可以看出,虽然从离散的形式变成了连续的形式,但是我们学习的目标都是一致的,也就是用一个网络来学习分布的 score function。得到 score function 之后我们就可以从反向 SDE 中进行采样,采样的方法也并不唯一,最简单的一种方法是 Euler-Maruyama 方法: \[ \begin{aligned} \Delta\mathbf{x}&\leftarrow[\mathbf{f}(\mathbf{x},t)-g^2(t)\mathbf{s}_\theta(\mathbf{x},t)]\Delta t+g(t)\sqrt{|\Delta t|}\mathbf{z}_t\\ \mathbf{x}&\leftarrow\mathbf{x}+\Delta\mathbf{x}\\ t&\leftarrow t+\Delta t \end{aligned} \] 其中 \(\mathbf{z}\sim\mathcal{N}(0,I)\),可以通过直接对高斯噪声采样得到。上式中的 \(f(\mathbf{x},t)\) 和 \(g(t)\) 都是有解析形式的,\(\Delta t\) 可以选取一个比较小的值,只有 \(\mathbf{s}_\theta(\mathbf{x},t)\) 是参数模型。可以从下边的动图直观感受一下采样过程:
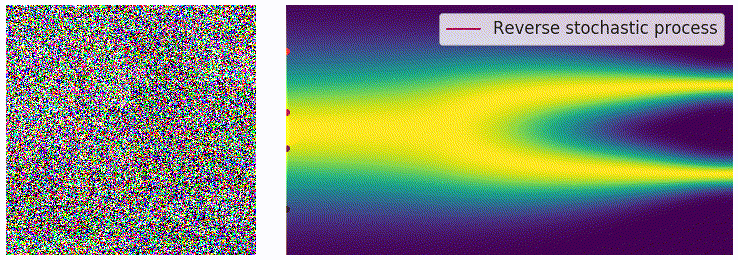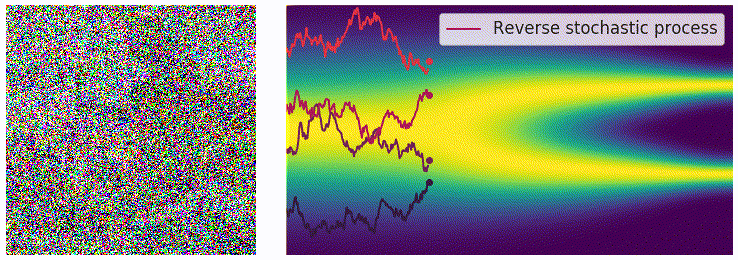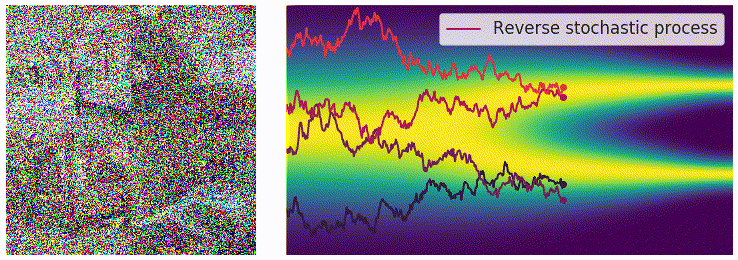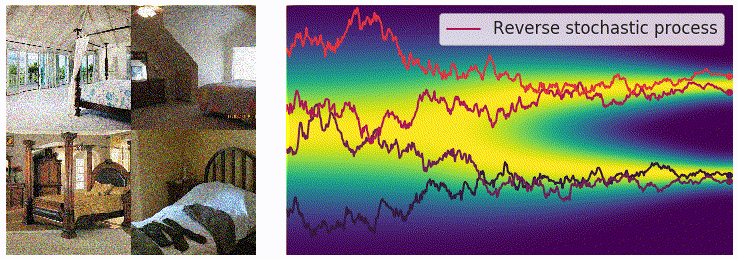
使用 score matching 进行训练
我们知道反向 SDE 采样的过程中,需要学习的也是 score function \(\mathbf{s}_\theta(\mathbf{x},t)\approx\nabla_\mathbf{x}\log p_t(\mathbf{x})\),那么为了对其进行估计,同样可以使用 score matching 的方式进行训练。和上一篇文章中介绍的类似,优化的目标为: \[ \mathbb{E}_{t\in\mathcal{U}(0,T)}\mathbb{E}_{p_t(\mathbf{x})}\left[\lambda(t)||\nabla_\mathbf{x}\log p_t(\mathbf{x})-\mathbf{s}_\theta(\mathbf{x},t)||_2^2\right] \] 可以看到依然是使用 L2 损失进行优化,只不过不再是简单地对所有的噪声进行求和,而是改为了计算均匀时间分布 \([0,T]\) 范围内损失的期望。另一个不同是权重的选取变为了 \(\lambda(t)\propto 1/\mathbb{E}[||\nabla_{\mathbf{x}(t)}\log p(\mathbf{x}(t)|\mathbf{x}(0))||_2^2]\)。用这种方式训练后,我们便得到了可以用于采样的 score function。
另一个比较值得讨论的点是,在离散的情况下,\(\lambda(t)\) 的选取是 \(\lambda(t)=\sigma_t^2\),如果我们在这里也使用类似的形式,也就是 \(\lambda(t)=g^2(t)\),可以推导出 \(p_0(\mathbf{x})\) 和 \(p_\theta(\mathbf{x})\) 之间的 KL 散度和上述损失之间的关系: \[ \mathrm{KL}(p_0(\mathbf{x})||p_\theta(\mathbf{x}))\le\frac{T}{2}\mathbb{E}_{t\in\mathcal{U}(0,T)}\mathbb{E}_{p_t(\mathbf{x})}\left[\lambda(t)||\nabla_\mathbf{x}\log p_t(\mathbf{x})-\mathbf{s}_\theta(\mathbf{x},t)||_2^2\right]+\mathrm{KL}(p_T||\pi) \] 这里的 \(\lambda(t)=g^2(t)\) 被称作 likelihood weighting function,通过使用这个加权函数,可以学习到非常好的分布。从这个角度来说,连续的表示方式和离散的表示方式依然是统一的。
讨论
其实介绍完上述的内容之后,就已经建立起了完整的基于 SDE 的 score-based modeling 的框架了。不过关于这一框架还有一些可以讨论的内容,主要分为三个方面。
和 DDPM 的联系
通过上文的介绍,我们可以发现用 SDE 描述的 score-based model 和扩散模型有很多相似之处。在 DDPM 中,前向过程可以描述为以下形式: \[ \mathbf{x}_{t}=\sqrt{1-\beta_t}\mathbf{x}_{t-1}+\sqrt{\beta_t}\epsilon_{t-1},\quad\epsilon_{t-1}\sim\mathcal{N}(0,I) \] 这是一个离散的过程,\(t\in\{0,1,\cdots,T\}\)。由于 SDE 是连续的,需要将 DDPM 也转变为连续的形式,为此可以将所有时间步都除以 \(T\),即 \(t\in\{0,\frac{1}{T},\cdots,\frac{T-1}{T},1\}\),当 \(T\rightarrow\infty\),DDPM 就变成了一个连续的过程。代入上式,可以得到: \[ \mathbf{x}(t+\Delta t)=\sqrt{1-\beta(t+\Delta t)\Delta t}~\mathbf{x}(t)+\sqrt{\beta(t+\Delta t)\Delta t}~\epsilon(t) \] 泰勒展开后可以近似得到: \[ \begin{aligned} \mathbf{x}(t+\Delta t)&=\sqrt{1-\beta(t+\Delta t)\Delta t}~\mathbf{x}(t)+\sqrt{\beta(t+\Delta t)\Delta t}~\epsilon(t)\\ &\approx\mathbf{x}(t)-\frac{1}{2}\beta(t+\Delta t)\Delta t~\mathbf{x}(t)+\sqrt{\beta(t+\Delta t)\Delta t}~\epsilon(t)\\ &\approx\mathbf{x}(t)-\frac{1}{2}\beta(t)\Delta t\mathbf{x}(t)+\sqrt{\beta(t)\Delta t}\epsilon(t) \end{aligned} \] 当 \(T\rightarrow\infty\),即 \(\Delta t\rightarrow0\),有: \[ \mathrm{d}\mathbf{x}=-\frac{\beta(t)\mathbf{x}}{2}\mathrm{d}t+\sqrt{\beta(t)}\mathrm{d}\mathbf{w} \] 推导到这里可以发现,从 DDPM 的前向过程出发,得到了和 score-based model 形式相符的 SDE 方程,因此也可以使用 score matching、Langevin MCMC 等策略进行学习和采样。这里的推导比较简略,具体的可以看 Score-Based Generative Modeling through Stochastic Differential Equations 这篇文章的附录 B。
将 SDE 转化为 ODE 概率流
使用 Langevin MCMC 和 SDE 虽然可以获得比较好的采样效果,但是这两种方式都仅能对 log-likelihood 进行估计,无法对其精确计算。通过将 SDE 转化为 ODE,可以精确计算 log-likelihood。(感觉 SDE 和 ODE 的关系有点类似于 DDPM 和 DDIM 的关系)
通过一定的方式可以在不改变 \(p_t(\mathbf{x})\) 的概率分布的同时将 SDE 转化为 ODE: \[ \mathrm{d}\mathbf{x}=\left[\mathbf{f}(\mathbf{x},t)-\frac{1}{2}g^2(t)\nabla_\mathbf{x}\log p_t(\mathbf{x})\right]\mathrm{d}t \] 这两者的关系如下图所示,可以看出 ODE 概率流比 SDE 更加平滑,且最终得到的分布是和 SDE 相同的。因为 ODE 是确定性的,所以前向和反向过程都是可逆的,因此 ODE 概率流和 normalizing flow 有一些相似之处。关于 normalizing flow 的介绍可以看我之前的文章,有比较详细的介绍。
条件生成
由于 DDPM 不容易推导出条件概率的形式,所以使用 DDPM 进行条件生成是比较难以显式地推导出实现方式的(不过也并非不能使用 DDPM 进行条件生成,我们后边会介绍 classifier guidance,就是用隐式的方式实现了对 DDPM 条件概率的求解)。由于 SDE 不存在这个问题,所以可以显式地解决条件生成的问题。
形式化地来说,给定随机变量 \(\mathbf{y}\) 和 \(\mathbf{x}\),已知前向过程的概率分布 \(p(\mathbf{y}|\mathbf{x})\),以 \(\mathbf{y}\) 为条件生成 \(\mathbf{x}\) 可以表示为: \[ p(\mathbf{x}|\mathbf{y})=\frac{p(\mathbf{x})p(\mathbf{y}|\mathbf{x})}{\int p(\mathbf{x})p(\mathbf{y}|\mathbf{x})\mathrm{d}\mathbf{x}} \] 两侧求梯度,得到: \[ \nabla_\mathbf{x}\log p(\mathbf{x}|\mathbf{y})=\nabla_\mathbf{x}\log p(\mathbf{x})+\nabla_\mathbf{x}\log p(\mathbf{y}|\mathbf{x}) \] 由于 \(\nabla_\mathbf{x}\log p(\mathbf{x})\) 可以通过 score matching 进行建模,且已知 \(p(\mathbf{y}|\mathbf{x})\),那么先验分布 \(\nabla_\mathbf{x}\log p(\mathbf{y}|\mathbf{x})\) 也是比较容易求得的,因此可以求得后验分布的梯度 \(\nabla_\mathbf{x}\log p(\mathbf{x}|\mathbf{y})\),再使用 Langevin MCMC 采样即可实现条件生成。
总结
本文中我们介绍了基于 SDE 进行 score-based 建模的方式,实际上相比于上一篇文章的内容来说,使用 SDE 主要的作用就是把离散形式的扰动过程变为了连续的形式,而训练方式、采样方式都和离散的形式大同小异。通过指定特定形式的 \(\mathbf{f}(\mathbf{x},t)\) 和 \(g(t)\),可以获得和 DDPM 相同的性质,而通过将 SDE 转化为 ODE,则与 normalizing flow 比较相似,可见 SDE 是一个比较通用的描述框架。
参考资料: