感谢 qq、wbs、hsh 等读者对本文提出的宝贵意见（大拍手

论文链接：Denoising Diffusion Probabilistic Models

端午假期卷一卷，开一个新坑系统性地整理一下扩散模型的相关知识。扩散模型的名字来源于物理中的扩散过程，对于一张图像来说，类比扩散过程，向这张图像逐渐加入高斯噪声，当加入的次数足够多的时候，图像中像素的分布也会逐渐变成一个高斯分布。当然这个过程也可以反过来，如果我们设计一个神经网络，每次能够从图像中去掉一个高斯噪声，那么最后就能从一个高斯噪声得到一张图像。虽然一张有意义的图像不容易获得，但高斯噪声很容易采样，如果能实现这个逆过程，就能实现图像的生成。

DDPM 示意图

这个过程可以形象地用上图表示，扩散模型中有两个过程，分别是前向过程（从图像加噪得到噪音）和反向过程（从噪音去噪得到图像）。在上图中，向图像 \(\mathbf{x}_0\) 逐渐添加噪声可以得到一系列的 \(\mathbf{x}_1,\mathbf{x}_2,...,\mathbf{x}_T\)，最后的 \(\mathbf{x}_T\) 即接近完全的高斯噪声，这个过程显然是比较容易的。而从 \(\mathbf{x}_T\) 逐渐去噪得到 \(\mathbf{x}_0\)​ 并不容易，扩散模型学习的就是这个去噪的过程。

前向过程

我们从比较简单的前向过程开始，第一个问题是如何向图像中添加高斯噪声。在 DDPM 中，加噪的方式是直接对图像和标准高斯噪声 \(\epsilon_{t-1}\sim\mathcal{N}(0,\mathbf{I})\) 进行加权求和： \[ \mathbf{x}_{t}=\sqrt{1-\beta_t}\mathbf{x}_{t-1}+\sqrt{\beta_t}\epsilon_{t-1} \] 这里的 \(\beta_t\) 就是每一步加噪使用的方差，在实际上进行加噪时，起始时使用的方差比较小，随着加噪步骤增加，方差会逐渐增大。例如在 DDPM 的原文中，使用的方差是从 \(\beta_1=10^{-4}\) 随加噪时间步线性增大到 \(\beta_T=0.02\)。这样设置主要是为了方便模型进行学习，如果在最开始就加入很大的噪声，对图像信息的破坏会比较严重，不利于模型学习图像的信息。这个过程也可以从反向进行理解，即去噪时先去掉比较大的噪音得到图像的雏形，再去掉小噪音进行细节的微调。

在上边的公式里，我们可以认为 \(\mathbf{x}_t\) 满足均值为 \(\sqrt{1-\beta_t}\mathbf{x}_{t-1}\)，标准差为 \(\sqrt{\beta_t}\mathbf{I}\) 的高斯分布。这样可以把上述加权求和的过程写成条件概率分布的形式： \[ q(\mathbf{x}_t|\mathbf{x}_{t-1})=\mathcal{N}(\mathbf{x}_t;\sqrt{1-\beta_t}\mathbf{x}_{t-1},\beta_t\mathbf{I}) \] 上边等号的右边表示的就是当前的变量 \(\mathbf{x}_t\) 满足一个 \(\mathcal{N}(\sqrt{1-\beta_t}\mathbf{x}_{t-1},\beta_t\mathbf{I})\) 的概率分布。通过上边的公式我们可以看到，每一个时间步的 \(\mathbf{x}_t\) 都只和 \(\mathbf{x}_{t-1}\) 有关，因此这个扩散过程是一个马尔可夫过程。在前向过程中，每一步的 \(\beta\) 都是固定的，真正的变量只有 \(\mathbf{x}_{t-1}\)，那么我们可以将公式中的 \(\mathbf{x}_{t-1}\) 进一步展开： \[ \begin{aligned} \mathbf{x}_t&=\sqrt{1-\beta_t}\mathbf{x}_{t-1}+\sqrt{\beta_t}\epsilon_{t-1}\\ &=\sqrt{1-\beta_t}(\sqrt{1-\beta_{t-1}}\mathbf{x}_{t-2}+\sqrt{\beta_{t-1}}\epsilon_{t-2})+\sqrt{\beta_t}\epsilon_{t-1}\\ &=\sqrt{(1-\beta_t)(1-\beta_{t-1})}\mathbf{x}_{t-2}+\sqrt{(1-\beta_t)\beta_{t-1}}\epsilon_{t-2}+\sqrt{\beta_t}\epsilon_{t-1} \end{aligned} \] 在上边的公式里，实际上 \(\epsilon_{t-2}\) 和 \(\epsilon_{t-1}\) 是同分布的，都是 \(\mathcal{N}(0,1)\)，因此可以进行合并： \[ \begin{aligned} \mathbf{x}_t&=\sqrt{(1-\beta_t)(1-\beta_{t-1})}\mathbf{x}_{t-2}+\sqrt{(\sqrt{(1-\beta_t)\beta_{t-1}})^2+(\sqrt{\beta_t})^2}\bar{\epsilon}_{t-2}\\ &=\sqrt{(1-\beta_t)(1-\beta_{t-1})}\mathbf{x}_{t-2}+\sqrt{1-(1-\beta_t)(1-\beta_{t-1})}\bar{\epsilon}_{t-2} \end{aligned} \] 令 \(\alpha_t=1-\beta_t\)，\(\bar{\alpha}_t=\prod_{i=1}^t\alpha_i\)，继续推导，可以得到： \[ \begin{aligned} \mathbf{x}_t&=\sqrt{\alpha_t\alpha_{t-1}}\mathbf{x}_{t-2}+\sqrt{1-\alpha_t\alpha_{t-1}}\bar{\epsilon}_{t-2}\\ &=\cdots\\ &=\sqrt{\bar{\alpha}_t}\mathbf{x}_0+\sqrt{1-\bar{\alpha}_t}\epsilon \end{aligned} \] 通过上述的推导，我们发现给定 \(\mathbf{x}_0\) 和加噪的时间步，可以直接用一步就得到 \(\mathbf{x}_t\)，而并不需要一步步地重复最开始的加权求和。和上述同理，这个关系也可以写成： \[ q(\mathbf{x}_t|\mathbf{x}_0)=\mathcal{N}(\mathbf{x}_t;\sqrt{\bar{\alpha}_t}\mathbf{x}_0,(1-\bar{\alpha}_t)\mathbf{I}) \] 从这个式子里我们可以看出，加噪过程中的 \(\mathbf{x}_t\) 可以看作原始图像 \(\mathbf{x}_0\) 和高斯噪声 \(\epsilon\) 的线性组合，且两个组合系数的平方和为 1。在实现加噪过程时，加噪的 scheduler 也是根据 \(\bar{\alpha}_t\) 设计的，这样更加直接，且为了保证最后得到的足够接近噪声，可以将 \(\bar\alpha_t\) 直接设置为一个接近 0 的数。

反向过程

正如文章开始所说的，反向过程就是从 \(\mathbf{x}_T\) 逐渐去噪得到 \(\mathbf{x}_0\) 的过程，也就是求 \(q(\mathbf{x}_{t-1}|\mathbf{x}_t)\)。根据贝叶斯公式： \[ q(\mathbf{x}_{t-1}|\mathbf{x}_t)=\frac{q(\mathbf{x}_t|\mathbf{x}_{t-1})q(\mathbf{x}_{t-1})}{q(\mathbf{x}_t)} \] 在上边的公式里，在前文中我们已经给出了 \(q(\mathbf{x}|\mathbf{x}_{t-1})\)，但 \(q(\mathbf{x}_{t-1})\) 和 \(q(\mathbf{x}_t)\) 依然是未知的。虽然这两个分布目前未知，但是在上一节的最后，我们已经推导出了 \(q(\mathbf{x}_t|\mathbf{x}_0)\) 这个分布，那么我们可以给上面的贝叶斯公式加上 \(\mathbf{x}_0\) 作为条件，将等号右侧的两个未知分布转化为已知分布： \[ q(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0)=\frac{q(\mathbf{x}_t|\mathbf{x}_{t-1},\mathbf{x}_0)q(\mathbf{x}_{t-1}|\mathbf{x}_0)}{q(\mathbf{x}_t|\mathbf{x}_0)} \] 而且因为先验分布 \(q(\mathbf{x}_t|\mathbf{x}_{t-1})\) 是马尔可夫过程，\(\mathbf{x}_t\) 只与 \(\mathbf{x}_{t-1}\) 有关，而与 \(\mathbf{x}_0\) 无关，所以上边式子里的 \(q(\mathbf{x}_t|\mathbf{x}_{t-1},\mathbf{x}_0)=q(\mathbf{x}_t|\mathbf{x}_{t-1})\)。但推导到这里还有问题，我们把 \(\mathbf{x}_0\) 加入到了条件概率分布的条件中，但 \(\mathbf{x}_0\) 依然是未知的，因此我们需要继续推导出一个与 \(\mathbf{x}_0\) 无关的式子。

上面的公式右侧的几个条件概率分布全都是高斯分布： \[ \begin{aligned} q(\mathbf{x}_t|\mathbf{x}_{t-1})&=\mathcal{N}(\mathbf{x}_t;\sqrt{\alpha_t}\mathbf{x}_{t-1},1-\alpha_t)\\ q(\mathbf{x}_{t-1}|\mathbf{x}_0)&=\mathcal{N}(\mathbf{x}_{t-1};\sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_0,1-\bar{\alpha}_{t-1})\\ q(\mathbf{x}_t|\mathbf{x}_0)&=\mathcal{N}(\mathbf{x}_t;\sqrt{\bar{\alpha}_t}\mathbf{x}_0,1-\bar\alpha_t) \end{aligned} \] 用概率密度函数把这个公式展开，如果不看前边的常数项，可以得到： \[ \begin{aligned} q(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0)&\propto\exp\left(-\frac{1}{2}\left[\frac{(\mathbf{x}_t-\sqrt{\alpha_t}\mathbf{x}_{t-1})^2}{\beta_t}+\frac{(\mathbf{x}_{t-1}-\sqrt{\bar\alpha_{t-1}}\mathbf{x}_0)^2}{1-\bar\alpha_{t-1}}+\frac{(\mathbf{x}_t-\sqrt{\bar{\alpha}_t}\mathbf{x}_0)}{1-\bar\alpha_t}\right]\right)\\ \end{aligned} \] 因为我们在这一步去噪的时候想求得的是 \(\mathbf{x}_{t-1}\) 的分布，所以我们把上式展开并整理成一个关于 \(\mathbf{x}_{t-1}\) 的多项式： \[ q(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0)\propto\exp\left(-\frac{1}{2}\left[\left(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar\alpha_{t-1}}\right)\mathbf{x}_{t-1}^2-\left(\frac{2\sqrt{\alpha_t}}{\beta_t}\mathbf{x}_t+\frac{2\sqrt{\bar\alpha_{t-1}}}{1-\bar\alpha_{t-1}}\mathbf{x}_0\right)\mathbf{x}_{t-1}+C(\mathbf{x}_t,\mathbf{x}_0)\right]\right) \] 上边的式子里常数项不重要（因为可以直接变成常数从指数部分挪走），所以可以暂时不管。对比高斯分布（可以证明反向过程的分布也是高斯分布）的指数部分 \(\exp\left(-\frac{1}{2}\left(\frac{1}{\sigma^2}x^2-\frac{2\mu}{\sigma^2}x+\frac{\mu^2}{\sigma^2}\right)\right)\)： \[ \begin{cases} \begin{aligned} \frac{1}{\sigma^2}&=\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar\alpha_{t-1}}\\ \frac{2\mu}{\sigma^2}&=\frac{2\sqrt{\alpha_t}}{\beta_t}\mathbf{x}_t+\frac{2\sqrt{\bar\alpha_{t-1}}}{1-\bar\alpha_{t-1}}\mathbf{x}_0 \end{aligned} \end{cases} \] 可以发现 \(\sigma\) 的表达式里都是我们 scheduler 里的定值，而求解出均值 \(\mu\)： \[ \mu=\frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}\mathbf{x}_t+\frac{\sqrt{\bar\alpha_{t-1}}\beta_t}{1-\bar\alpha_t}\mathbf{x}_0 \] 代入上一章最后的 \(\mathbf{x}_t=\sqrt{\bar{\alpha}_t}\mathbf{x}_0+\sqrt{1-\bar{\alpha}_t}\epsilon\)，得到： \[ \mu=\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar\alpha_t}}\tilde{\epsilon}\right) \] 注意在反向过程中我们并不知道在前向过程中加入的噪声 \(\epsilon\) 是 \(\mathcal{N}(0,1)\) 中的具体哪一个噪声，而噪声也没有办法继续转换成其他的形式。因此我们使用神经网络在反向过程中估计的目标就是 \(\tilde{\epsilon}\)。在这个网络中，输入除了 \(\mathbf{x}_t\) 之外还需要 \(t\)，可以简单理解为：加噪过程中 \(\mathbf{x}_t\) 的噪声含量是由 \(t\) 决定的，因此在预测噪声时也需要知道时间步 \(t\)​ 作为参考，以降低预测噪声的难度。

注：关于反向过程为什么要这样做，Lilian Weng 基于变分推断给出了一个复杂的证明，因为过于难以理解，这里暂且把它跳过。（以后有可能会填坑，也有可能不会x）

具体的训练过程

我们已经知道了去噪网络的参数和预测目标，下一个问题就是如何去训练这个去噪网络。原始论文中给出了如下的训练过程：

DDPM 的训练过程

在上面的算法中，首先从数据集 \(q(\mathbf{x}_0)\) 中采样出 \(\mathbf{x}_0\)，从 1 到 T 的均匀分布中采样出 \(t\)，从标准高斯分布中采样出 \(\epsilon\)。然后根据 \(\mathbf{x}_t=\sqrt{\bar{\alpha}_t}\mathbf{x}_0+\sqrt{1-\bar{\alpha}_t}\epsilon\) 将 \(\mathbf{x}_0\) 与 \(\epsilon\) 加权求和得到噪声图，最后将噪声图和时间步输入到网络中预测噪声，并用真实的噪声计算出 L2 损失进行优化。

这里比较难理解的是 \(\epsilon\) 本身就是从标准高斯分布中采样出的，为什么还需要一个网络专门对其进行预测。我个人的理解是：尽管每次添加的噪声都是从固定的分布中采样出的，但如果用同一个分布中的另一个采样出的样本将其代替，就会向去噪过程引入一定的误差，最后这些误差积累的结果会破坏最终生成的图像。

具体的采样过程

论文中同样也给出了采样过程：

DDPM 的训练过程

具体来说，首先从标准正态分布中采样出 \(\mathbf{x}_T\) 作为初始的图像，然后重复 \(T\) 步去噪过程。在每一步去噪过程中，由于我们已经推导出： \[ q(\mathbf{x}_{t-1}|\mathbf{x}_t)=\mathcal{N}\left(\mathbf{x}_{t-1};\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar\alpha_t}}\tilde{\epsilon}\right),\sigma_t^2\right) \] 利用一个重参数化技巧：从 \(\mathcal{N}(\mu,\sigma^2)\) 采样可以实现为从 \(\mathcal{N}(0,1)\) 采样出 \(\epsilon\)，再计算 \(\mu+\epsilon\cdot\sigma\)。这样即可实现从上述的高斯分布中采样出 \(\mathbf{x}_{t-1}\)。如此重复 \(T\) 次即可得到最终的结果，注意最后一步的时候没有采样，而是只加上了均值。

DDPM 的代码实现

现有的主流方法使用 UNet 来实现去噪网络，如下图所示。

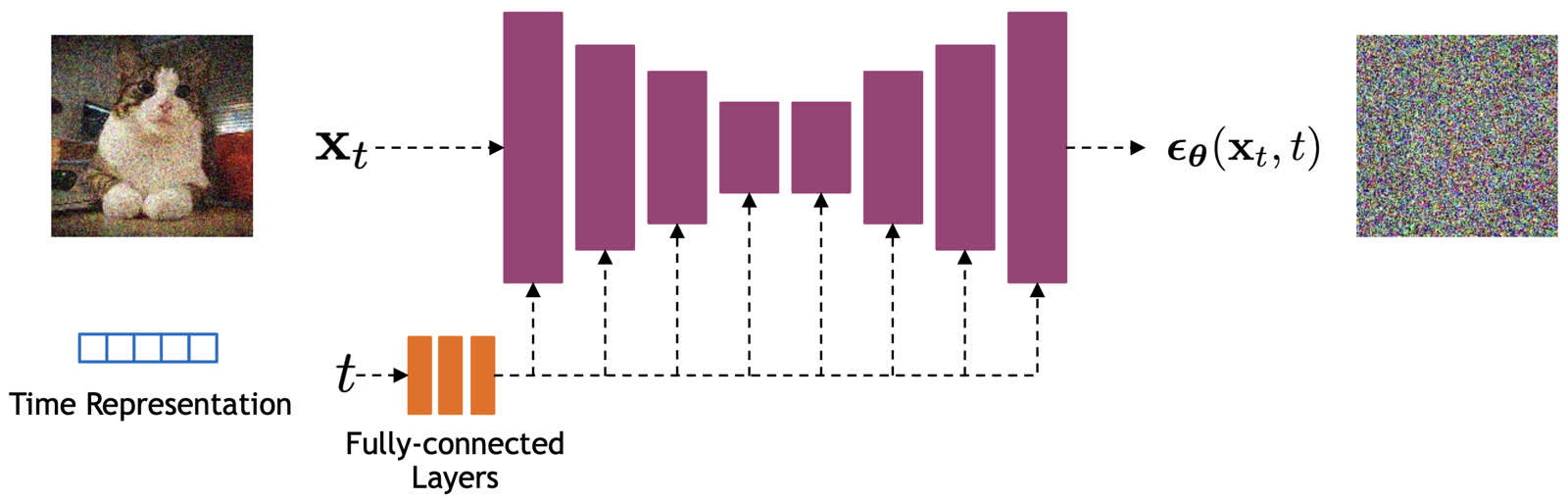
去噪网络的结构

为了降低理解的难度，我们这里不关心这个去噪网络的具体实现，只需要知道这个网络接收一个噪声图 \(\mathbf{x}_t\) 和一个时间步 \(t\) 作为参数，并输出一个噪声的预测结果 \(\epsilon_\theta(\mathbf{x}_t,t)\)。在 diffusers 库中已经实现了一个 2D UNet 网络，我们直接使用即可。下面我们也主要使用 diffusers 实现 DDPM 模型。

训练参数

首先配置训练的参数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from dataclasses import dataclass

@dataclass
class TrainingConfig:
    image_size = 64
    train_batch_size = 16
    eval_batch_size = 16
    num_epochs = 50
    gradient_accumulation_steps = 1
    learning_rate = 1e-4
    lr_warmup_steps = 500
    mixed_precision = "fp16"
    output_dir = "ddpm-animefaces-64"
    overwrite_output_dir = True

config = TrainingConfig()

训练数据

我们使用 huggan/anime-faces 数据集，这个数据集由 21551 张分辨率为 64x64 的动漫人物头像组成。我们加载这个数据集：

1
2
3
4
from datasets import load_dataset

dataset = load_dataset("huggan/anime-faces", split="train")
dataset = dataset.select(range(21551))

由于这个数据集的作者组织数据的方式不太规范，所以最后加载进来实际上数据集的长度是 86204，也就是 21551 张图片每张重复了 4 次，我们只需要保留前 21551 个样本即可。

然后为数据集设置预处理函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from torchvision import transforms

def get_transform():
    preprocess = transforms.Compose([
        transforms.Resize(config.image_size),
        transforms.ToTensor(),
        transforms.Normalize([0.5], [0.5]),
    ])
    def transform(samples):
        images = [preprocess(img.convert("RGB")) for img in samples["image"]]
        return dict(images=images)
    return transform

dataset.set_transform(get_transform())

最后创建 dataloader：

1
2
3
from torch.utils.data import DataLoader

dataloader = DataLoader(dataset, batch_size=config.train_batch_size, shuffle=True)

降噪网络

我们可以直接用 diffusers 创建降噪网络：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from diffusers import UNet2DModel

model = UNet2DModel(
    sample_size=config.image_size,
    in_channels=3,
    out_channels=3,
    layers_per_block=2,
    block_out_channels=(128, 128, 256, 256, 512, 512),
    down_block_types=(
        "DownBlock2D",
        "DownBlock2D",
        "DownBlock2D",
        "DownBlock2D",
        "AttnDownBlock2D",
        "DownBlock2D",
    ),
    up_block_types=(
        "UpBlock2D",
        "AttnUpBlock2D",
        "UpBlock2D",
        "UpBlock2D",
        "UpBlock2D",
        "UpBlock2D",
    ),
)

核心代码

前边的三个部分分别配置了一些训练参数，以及训练数据和模型，这些都是比较工程化的部分，而我们在上面推导的 DDPM 核心算法还没有实现。在这一小节我们主要来实现核心的算法。

首先我们需要先定义 \(\beta\)、\(\alpha\)，以及 \(\bar\alpha\) 等最基本的常量，这里我们保持 DDPM 原论文的配置，也就是 \(\beta\) 初始为 \(1\times10^{-4}\)，最终为 \(0.02\)，且共有 \(1000\) 个时间步：

1
2
3
4
5
6
7
8
9
10
11
12
13
import torch

class DDPM:
    def __init__(
        self,
        num_train_timesteps:int = 1000,
        beta_start: float = 0.0001,
        beta_end: float = 0.02,
    ):
        self.betas = torch.linspace(beta_start, beta_end, num_train_timesteps, dtype=torch.float32)
        self.alphas = 1.0 - self.betas
        self.alphas_cumprod = torch.cumprod(self.alphas, dim=0)
        self.timesteps = torch.arange(num_train_timesteps - 1, -1, -1)

然后是比较简单的前向过程，只需要实现加噪即可，按照 \(\mathbf{x}_t=\sqrt{\bar{\alpha}_t}\mathbf{x}_0+\sqrt{1-\bar{\alpha}_t}\epsilon\) 这个公式实现即可。注意需要将系数的维度数量都与输入样本对齐：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class DDPM:
    ...

    def add_noise(
        self,
        original_samples: torch.Tensor,
        noise: torch.Tensor,
        timesteps: torch.Tensor,
    ):
        alphas_cumprod = self.alphas_cumprod.to(device=original_samples.device ,dtype=original_samples.dtype)
        noise = noise.to(original_samples.device)
        timesteps = timesteps.to(original_samples.device)

        # \sqrt{\bar\alpha_t}
        sqrt_alpha_prod = alphas_cumprod[timesteps].flatten() ** 0.5
        while len(sqrt_alpha_prod.shape) < len(original_samples.shape):
            sqrt_alpha_prod = sqrt_alpha_prod.unsqueeze(-1)

        # \sqrt{1 - \bar\alpha_t}
        sqrt_one_minus_alpha_prod = (1.0 - alphas_cumprod[timesteps]).flatten() ** 0.5
        while len(sqrt_one_minus_alpha_prod.shape) < len(original_samples.shape):
            sqrt_one_minus_alpha_prod = sqrt_one_minus_alpha_prod.unsqueeze(-1)

        return sqrt_alpha_prod * original_samples + sqrt_one_minus_alpha_prod * noise

反向过程相对来说比较复杂，不过因为我们已经完成了公式的推导，只需要按照公式实现即可。我们也再把公式贴到这里，对着公式实现具体的代码： \[ \begin{aligned} \sigma&=\left(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar\alpha_{t-1}}\right)^{-1/2}\\ \mu&=\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar\alpha_t}}\tilde{\epsilon}_t\right) \end{aligned} \]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class DDPM:
    ...

    @torch.no_grad()
    def sample(
        self,
        unet: UNet2DModel,
        batch_size: int,
        in_channels: int,
        sample_size: int,
    ):
        betas = self.betas.to(unet.device)
        alphas = self.alphas.to(unet.device)
        alphas_cumprod = self.alphas_cumprod.to(unet.device)
        timesteps = self.timesteps.to(unet.device)
        images = torch.randn((batch_size, in_channels, sample_size, sample_size), device=unet.device)
        for timestep in tqdm(timesteps, desc='Sampling'):
            pred_noise: torch.Tensor = unet(images, timestep).sample

            # mean of q(x_{t-1}|x_t)
            alpha_t = alphas[timestep]
            alpha_cumprod_t = alphas_cumprod[timestep]
            sqrt_alpha_t = alpha_t ** 0.5
            one_minus_alpha_t = 1.0 - alpha_t
            sqrt_one_minus_alpha_cumprod_t = (1 - alpha_cumprod_t) ** 0.5
            mean = (images - one_minus_alpha_t / sqrt_one_minus_alpha_cumprod_t * pred_noise) / sqrt_alpha_t

            # variance of q(x_{t-1}|x_t)
            if timestep > 0:
                beta_t = betas[timestep]
                one_minus_alpha_cumprod_t_minus_one = 1.0 - alphas_cumprod[timestep - 1]
                one_divided_by_sigma_square = alpha_t / beta_t + 1.0 / one_minus_alpha_cumprod_t_minus_one
                variance = (1.0 / one_divided_by_sigma_square) ** 0.5
            else:
                variance = torch.zeros_like(timestep)

            epsilon = torch.randn_like(images)
            images = mean + variance * epsilon
        images = (images / 2.0 + 0.5).clamp(0, 1).cpu().permute(0, 2, 3, 1).numpy()
        return images

训练与推理

最后是训练和推理的代码，这部分也比较工程，直接套用现成代码即可：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
from accelerate import Accelerator
from diffusers.optimization import get_cosine_schedule_with_warmup
from diffusers.utils import make_image_grid, numpy_to_pil
import torch.nn.functional as F
import os

model = model.cuda()
ddpm = DDPM()
optimizer = torch.optim.AdamW(model.parameters(), lr=config.learning_rate)
lr_scheduler = get_cosine_schedule_with_warmup(
    optimizer=optimizer,
    num_warmup_steps=config.lr_warmup_steps,
    num_training_steps=(len(dataloader) * config.num_epochs),
)
accelerator = Accelerator(
    mixed_precision=config.mixed_precision,
    gradient_accumulation_steps=config.gradient_accumulation_steps,
    log_with="tensorboard",
    project_dir=os.path.join(config.output_dir, "logs"),
)
model, optimizer, dataloader, lr_scheduler = accelerator.prepare(
    model, optimizer, dataloader, lr_scheduler
)
global_step = 0
for epoch in range(config.num_epochs):
    progress_bar = tqdm(total=len(dataloader), disable=not accelerator.is_local_main_process, desc=f'Epoch {epoch}')

    for step, batch in enumerate(dataloader):
        clean_images = batch["images"]
        # Sample noise to add to the images
        noise = torch.randn(clean_images.shape, device=clean_images.device)
        bs = clean_images.shape[0]
        # Sample a random timestep for each image
        timesteps = torch.randint(
            0, ddpm.num_train_timesteps, (bs,), device=clean_images.device,
            dtype=torch.int64
        )
        # Add noise to the clean images according to the noise magnitude at each timestep
        noisy_images = ddpm.add_noise(clean_images, noise, timesteps)
        with accelerator.accumulate(model):
            # Predict the noise residual
            noise_pred = model(noisy_images, timesteps, return_dict=False)[0]
            loss = F.mse_loss(noise_pred, noise)
            accelerator.backward(loss)
            accelerator.clip_grad_norm_(model.parameters(), 1.0)
            optimizer.step()
            lr_scheduler.step()
            optimizer.zero_grad()
        progress_bar.update(1)
        logs = {"loss": loss.detach().item(), "lr": lr_scheduler.get_last_lr()[0], "step": global_step}
        progress_bar.set_postfix(**logs)
        accelerator.log(logs, step=global_step)
        global_step += 1

    if accelerator.is_main_process:
        # evaluate
        images = ddpm.sample(model, config.eval_batch_size, 3, config.image_size)
        image_grid = make_image_grid(numpy_to_pil(images), rows=4, cols=4)
        samples_dir = os.path.join(config.output_dir, 'samples')
        os.makedirs(samples_dir, exist_ok=True)
        image_grid.save(os.path.join(samples_dir, f'{global_step}.png'))
        # save models
        model.save_pretrained(config.output_dir)

结果展示

训练在一张 NVIDIA GeForce RTX 4090 GPU 上大概需要运行 3 个多小时，最后的结果大概长这个样子：

生成结果示例

可以看到虽然里边难免有一些比较奇形怪状的结果，不过总体上来说已经初具雏形了。

总结

本文总结了 DDPM 的理论和实现方式，在代码部分我们是完全根据推导出的公式实现的采样过程。实际上在很多代码库中，采样过程并没有严格按照论文中的公式实现，而是先从 \(\mathbf{x}_t\)、\(t\) 和预测的噪声反向计算出 \(\mathbf{x}_0\)，再基于 \(\mu=\frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}\mathbf{x}_t+\frac{\sqrt{\bar\alpha_{t-1}}\beta_t}{1-\bar\alpha_t}\mathbf{x}_0\) 计算均值，这样的好处在于可以对 \(\mathbf{x}_0\) 进一步规范化，控制输出的范围。

可以看出 DDPM 虽然理论比较复杂，但实现起来还是比较简单直接的。因为作者本人对 diffusion models 的理解也不算非常深入，所以如果文章有问题的话欢迎各位读者来讨论，后续（如果没有鸽掉的话）还会更新一些其他的 diffusion models 的文章，欢迎追更）

本文完整的代码以及训练好的模型见如下链接：

参考资料：

  1. 简单基础入门理解Denoising Diffusion Probabilistic Model，DDPM扩散模型
  2. 扩散模型之DDPM
  3. Denoising Diffusion-based Generative Modeling: Foundations and Applications
  4. Train a diffusion model