笔记|Normalizing Flow 理论与实现(一)基础理论
Normalizing flow(标准化流)是一类对概率分布进行建模的工具,它能完成简单的概率分布(例如高斯分布)和任意复杂分布之间的相互转换,经常被用于 data generation、density estimation、inpainting 等任务中,例如 Stability AI 提出的 Stable Diffusion 3 中用到的 rectified flow 就是 normalizing flow 的变体之一。
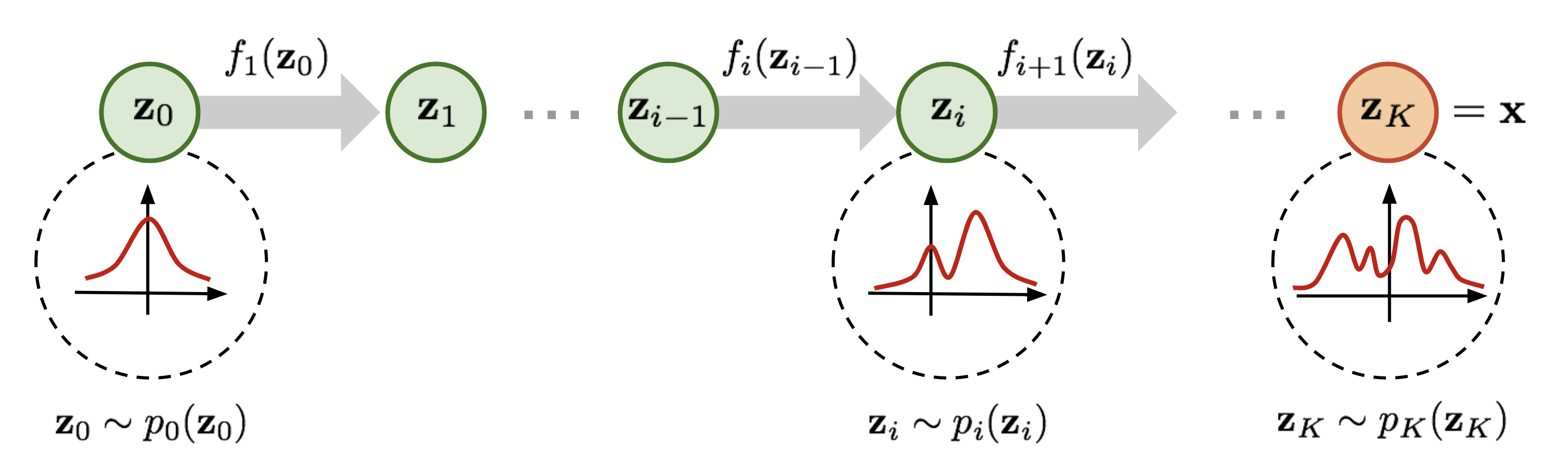
为了便于理解,在正式开始介绍之前先简要说明一下 normalizing flow 的做法。如上图所示,为了将一个高斯分布 \(z_0\) 转换为一个复杂的分布 \(z_K\),normalizing flow 会对初始的分布 \(z_0\) 进行多次可逆的变换,将其逐渐转换为 \(z_K\)。由于每一次变换都是可逆的,从 \(z_K\) 出发也能得到高斯分布 \(z_0\)。这样,我们就实现了复杂分布与高斯分布之间的互相转换,从而能从简单的高斯分布建立任意复杂分布。
对 diffusion models 比较熟悉的读者可能已经发现了,这个过程和 diffusion 的做法非常相似。在 diffusion model 中,对于一个从高斯分布中采样出的样本,模型也是通过一系列去噪过程,从而获得目标样本;同样也可以通过其逆过程从一个确定的样本通过加噪得到高斯噪声。这两者的确有一些相似之处,可以放到一起来了解。
概率密度映射的推导
因为 normalizing flow 构建复杂分布主要依靠概率分布的可逆映射,因此需要首先推导在映射的过程中,概率密度会发生怎样的变化。为了导出最终的结论,一个需要了解的概念是 Jacobian 矩阵,对于一个将 \(n\) 维向量变化为一个 \(m\) 维向量的变换 \(\mathbf{f}:\mathbb{R}^n\rightarrow\mathbb{R}^m\),其全部一阶偏导数构成的矩阵即为 Jacobian 矩阵 \(\mathbf{J}\): \[ \mathbf{J}=\begin{pmatrix} \frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\\\ \vdots & \ddots & \vdots \\\\ \frac{\partial f_m}{\partial x_1} & \cdots & \frac{\partial f_m}{\partial x_n} \end{pmatrix}. \]
对于给定的随机变量 \(z\) 以及其概率密度函数 \(z\sim\pi(z)\),构造一个双射 \(x=f(z)\),则同时也有 \(z=f^{-1}(x)\),下面我们来计算 \(x\) 的概率密度函数 \(p(x)\)。根据概率密度函数的定义,有: \[ \int p(x)\mathrm{d}x=\int\pi(z)\mathrm{d}z=1, \]
由于 \(x\) 和 \(z\) 满足双射,则任意 \(\mathrm{d}z\) 体积内包含的概率与其映射到的 \(\mathrm{d}x\) 内包含的概率是相等的,且概率密度处处大于 0,据此可以根据变量替换定理推导: \[ p(x)=\pi(z)\left|\frac{\mathrm{d}z}{\mathrm{d}x}\right|=\pi(f^{-1}(x))\left|\frac{\mathrm{d}f^{-1}}{\mathrm{d}x}\right|=\pi(f^{-1}(x))\left|(f^{-1})'(x)\right|. \]
对于高维随机变量 \(\mathbf{z}\sim\pi(\mathbf{z}),\ \mathbf{z}\in\mathbb{R}^n\) 以及多元函数 \(\mathbf{f}:\mathbb{R}^n\rightarrow\mathbb{R}^n\),也可以推导出类似的结论: \[ p(\mathbf{x})=\pi(\mathbf{z})\left|\mathrm{det}\ \frac{\mathrm{d}\mathbf{z}}{\mathrm{d}\mathbf{x}}\right|=\pi(\mathbf{f}^{-1}(\mathbf{x}))\left|\mathrm{det}\ \mathbf{J}(\mathbf{f}^{-1}(\mathbf{x}))\right|. \]
可以发现,对于已知的概率分布与双射,我们可以用一个带有 Jacobian 矩阵的式子来表示映射后的概率分布。我们可以从下面这个直观的例子来理解 Jacobian 矩阵在这里表示的含义:\(X_0\) 和 \(X_1\) 是两个随机变量,且满足 \(X_1=2X_0+2\),由于 \(X_0\) 的概率密度在 \((0,1)\) 间均匀分布,根据概率密度的性质,可知其概率密度处处为 1。对于 \(X_1\) 来说,其定义域是将 \(X_0\) 的定义域均匀扩大 2 倍得到的,那么其概率密度也应当减半。
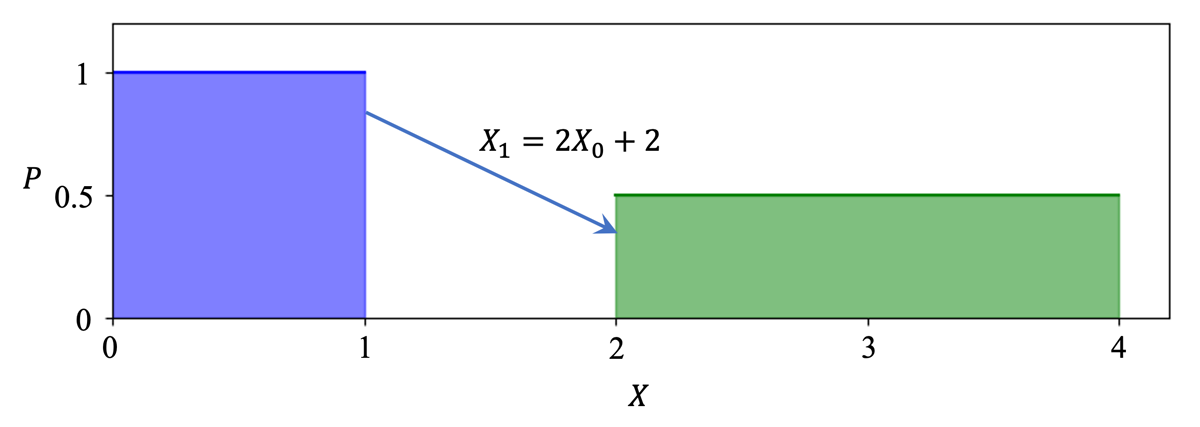
通过这个例子,可以对简单地理解 \(p(x)=\pi(f^{-1}(x))\left|(f^{-1})'(x)\right|\) 这一公式中 \(\left|(f^{-1})'(x)\right|\) 一项的含义:对于一个概率分布,其「单位体积」内所包含的概率是一定的,如果映射后「单位体积」的大小发生了变化,那么其概率密度也要相应地作出变化,来保证所含的概率不变。而且值得注意的是,在这个过程中我们只关心变化率的大小,而不关心变化率的方向(也就是导数的正负),因此这一项需要取绝对值。
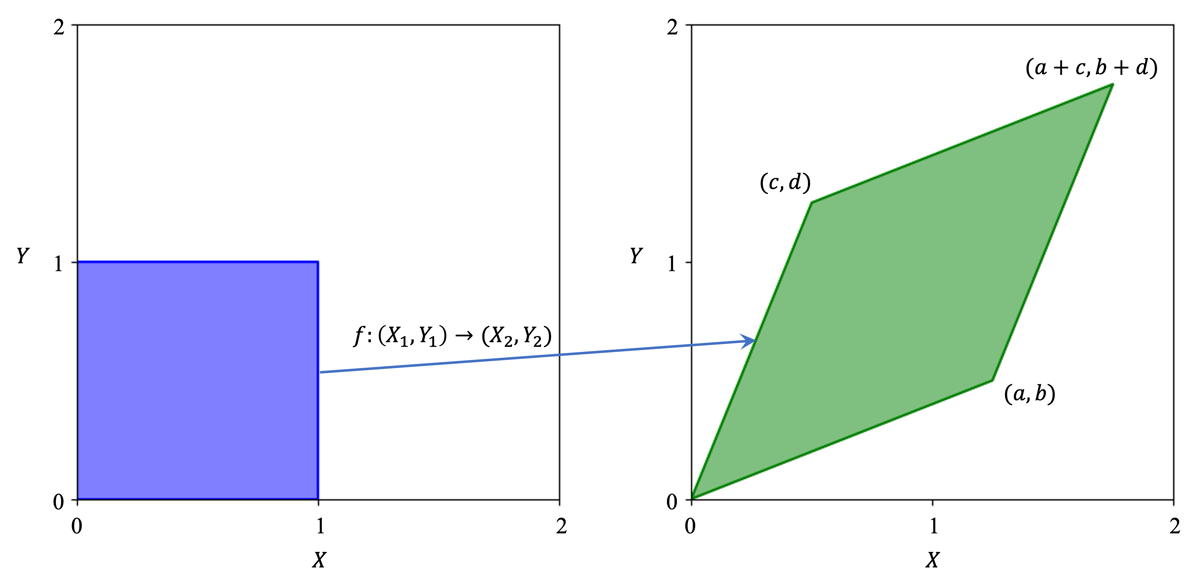
再举一个稍微复杂一点的例子:下图中蓝色的是在二维空间中均匀分布的二维随机变量 \((X_1, Y_1)\),可逆映射 \(f\) 将其映射到 \((X_2, Y_2)\)。我们不难得知代表 \(f\) 的变换矩阵就是 \(T=[[a,b];[c,d]]\),通过左乘 \(T\) 可以将任意 \((X_1,Y_1)\) 转换为对应的 \((X_2,Y_2)\)。与上一个例子同理,\((X_1,Y_1)\) 的概率密度处处为 1,而 \((X_2,Y_2)\) 的概率密度则需要用 1 除以绿色平行四边形的面积,即 \(ad-bc\)。这个值同时也是变换矩阵 \(T\) 的行列式的值,由此我们可以发现,Jacobian 矩阵的行列式的绝对值就是概率密度的变化率。
回到 Normalizing Flow
现在我们已经推导出概率密度的映射关系,那么 normalizing flow 的做法就已经呼之欲出了。回到文章最开始的示意图,对于一个高斯分布 \(z_0\),我们可以通过一系列双射 \(f_1,...,f_K\) 对其进行变换,得到任意分布 \(z_K\),在这个分布里采样得到样本,就完成了生成的过程。在这一过程中,由概率密度变换公式两边取对数,可以得到:
\[ \begin{align*} p_i(\mathbf{z}_i)&=p_{i-1}(\mathbf{z}_{i-1}) \left| \mathrm{det} \frac{\mathrm{d}f_i}{\mathrm{d}\mathbf{z}_{i-1}} \right|^{-1} \\ \log p_i(\mathbf{z}_i)&=\log p_{i-1}(\mathbf{z}_{i-1}) - \log \left| \mathrm{det} \frac{\mathrm{d}f_i}{\mathrm{d}\mathbf{z}_{i-1}} \right| \end{align*} \]
将一系列这样的映射耦合起来,有 \(\mathbf{x}=\mathbf{z}_K=f_K\circ f_{K-1}\circ\cdots\circ f_1(\mathbf{z}_0)\),那么 \(p(\mathbf{x})\) 可以由下式求得:
\[ \log p(\mathbf{x})=\log \pi_0(\mathbf{z}_0)-\sum_{i=1}^K\log\left|\mathrm{det}\ \frac{\mathrm{d}f_i}{\mathrm{d}\mathbf{z}_{i-1}}\right| \]
这样一系列变换耦合的过程就是 flow,由于最终得到的是标准正态分布,所以是 normalizing flow。同时,基于上述描述,我们也可以得知变换 \(f\) 应该有以下两个性质:
- 其逆变换应当容易求得
- 其 Jacobian 矩阵的行列式应当容易求得
后续的文章将会介绍一些具体的 normalizing flow 模型及实现,敬请期待。
参考资料: